基本概念
頻率回響
頻率回響法(Frequency-response Analysis)是二十世紀三十年代發展起來的一種經典工程實用方法，是一種利用頻率特性進行控制系統分析的方法,可方便地用於控制工程中的系統分析與設計。
頻率回響是指系統在輸入正弦信號時的穩態正弦回響。
頻率特性
頻率特性是系統的頻率回響所反映出的特性。
分析系統頻率特性的原因是，控制系統中信號常常可以表示為不同頻率正弦信號的疊加，而頻率特性可以反映系統在正弦信號作用下的回響性能 。
奈奎斯特圖
奈奎斯特圖是用圖解法表現系統頻率特性的方法，將頻率回響通過其幅頻特性及相頻特性表示在極坐標中的圖形，稱為幅相圖，或奈奎斯特(Nyquist)圖。
圖解
如圖為典型慣性環節的奈奎斯特圖，
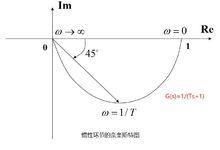奈奎斯特圖
奈奎斯特圖 奈奎斯特圖 奈奎斯特圖以為參變數，當從0到+∞ 時，G(j) 在複平面上的軌跡，就是頻率特性的極坐標圖，稱為Nyquist圖。
奈奎斯特圖上每一點都是對應一特定頻率下的頻率回響，該點相對於原點的角度表示相位，而和原點之間的距離表示增益，因此奈奎斯特圖將振幅及相位的波德圖綜合在一張圖中。
一般的系統有低通濾波器的特性，高頻時的頻率回響會衰減，增益降低，因此在奈奎斯特圖中會出現在較靠近原點的區域。
手繪作圖
手繪N圖的一般方法如下：
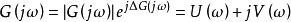奈奎斯特圖①將頻率特性表示這種形式：
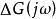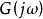奈奎斯特圖
奈奎斯特圖其中表示∠；
②計算Nyquist圖的起點(ω=0)和終點(ω→∞)的模、輻角、實部和虛部；
③計算特殊點坐標（包括與實軸交點、與虛軸交點、漸近線等）；
④根據所得點、漸近線輔助線等作出近似圖，由於開環奈奎斯特圖用於系統分析時不需要準確知道漸近線的位置，故一般取漸近線為坐標軸即可。
用途
閉環負反饋系統的穩定性評估可以由開環系統（同一個系統，但不考慮其反饋迴路）的 奈奎斯特圖，配合奈奎斯特穩定判據判斷其穩定性。此方法甚至可以用在有延遲的系統，或是傳遞函式不是有理函式的系統，這些系統用其他方法都很難分析。可以藉由圖線圍繞的次數及開環傳遞函式右半平面的極點數量來判斷穩定性。增益裕度可以用圖形越過實軸的數值（幅值裕度），或圖線穿過單位圓時的相位（相角裕度）來計算。
奈奎斯特圖可以提供一些有關傳遞函式的信息。例如曲線進入原點時的角度可以計算極點個數和零點個數的差。
當手繪奈奎斯特圖時，可以畫出圖形的外觀，但座標軸部份有些調整，以顯示一些重要部份的信息。當用計算機繪圖時，需要包括所有有關的頻率範圍，因此頻率可能會用對數的方式增加，以包括大的頻率範圍。
