簡介
在統計學中, 多元方差分析( MANOVA)是一種比較多變數樣本均值的程式 。作為一個多變數過程,它在有兩個或多個因變數時使用,並且通常後面是分別涉及各個因變數的顯著性檢驗。它有助於回答:
1)自變數的變化是否對因變數有顯著影響?
2)因變數之間的關係是什麼?
3)自變數之間有什麼關係?
與ANOVA的關係
MANOVA是單變數方差分析(ANOVA)的推廣形式,儘管與單變數ANOVA不同,它使用結果變數之間的協方差來檢驗平均差異的統計顯著性。其中,在單變數方差分析中出現平方和的情況下,在多變數方差分析中出現某些正定矩陣。對角線條目是出現在單變數ANOVA中的相同種類的平方和,非對角線條目則是相應的乘積和。在關於誤差分布的正態假設下,由於誤差導致的平方和對應部分服從Wishart分布。
 多元方差分析
多元方差分析 多元方差分析
多元方差分析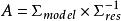 多元方差分析
多元方差分析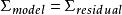 多元方差分析
多元方差分析 多元方差分析
多元方差分析MANOVA是基於模型方差矩陣,和誤差方差矩陣逆的乘積,即。假設,則。不變性考慮意味著MANOVA統計量應該是矩陣乘積奇異值分解的度量,但由於備選假設的多維性質,沒有唯一的選擇。
 多元方差分析
多元方差分析 多元方差分析
多元方差分析最常見的統計數據是基於 矩陣的根(或特徵值)的匯總:
 多元方差分析
多元方差分析 多元方差分析
多元方差分析 多元方差分析
多元方差分析 多元方差分析
多元方差分析因變數的相關性
多元方差分析效果受因變數的相關性和以及變數相關的效應大小的影響 。例如,當存在兩個組和兩個因變數時,當相關性等於較小標準化效應大小與較大標準化效應大小的比率時,多元方差分析效果最低。
