歷史
多元函式的概念很早就出現在物理學中,因為人們常常要研究取決於多個其他變數的物理量。例如托馬斯·布拉德華曾試圖尋找運動物體的速度、動力和阻力之間的關係。不過從十七世紀開始,這個概念有了長足發展。1667年,詹姆斯·格雷果里在 Vera circuli et hyperbolae quadratura一文中給出了多元函式最早的定義之一:“(多元)函式是由幾個量經過一系列代數運算或別的可以想像的運算得到的量。 ”十八世紀,人們發展了基於無窮小量的微積分,,並研究了常微分方程和偏微分方程的解法。那時多元函式的運算與一元函式類似。直到十九世紀末和二十世紀,人們才嚴格建立起偏導數(包括二階偏導數)的計算法則。
多元函式
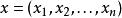 多元微積分
多元微積分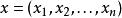 多元微積分
多元微積分 多元微積分
多元微積分 多元微積分
多元微積分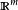 多元微積分
多元微積分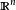 多元微積分
多元微積分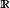 多元微積分
多元微積分多元函式是指定義域為 或其一部分,值域為 或 的函式。第二種情況可歸結為第一種情況,因為它實際上可看成m個定義在 上,值域是 的坐標函式。這樣的函式讓定義域中的每個元素(即 n元組)對應唯一一個值域中的元素,記為f(x)或,如下所示:
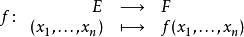 多元微積分
多元微積分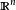 多元微積分
多元微積分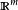 多元微積分
多元微積分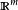 多元微積分
多元微積分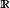 多元微積分
多元微積分如果線性空間和 上賦有範數,就可以研究這種多元函式的連續性和可微性。如果固定除一個變數外的其他變數,多元函式的研究就可歸結為值域是 的函式。如果分別考慮坐標函式的話,甚至可歸結為值域是 的函式。比如,這種函式的導數存在的話,就稱為原來多元函式的偏導數。
多元函式分析
數學分析中的經典概念可以推廣到多元函式,但也要引入線性代數中的概念。
極限與連續性
 多元微積分
多元微積分 多元微積分
多元微積分設E是中的一個開集,f是定義在E上的函式。給賦予一個範數之後,就可以這樣定義連續性:對E中的每個點a,f在a處連續若且唯若
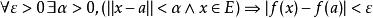 多元微積分
多元微積分在多元微積分領域,對函式極限和連續性的研究可導致許多違反直覺的結果。例如,一些二元標量函式,當x,y沿不同路徑(例如直線與拋物線)趨近於極限點時,函式的值不同。例如,函式
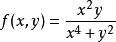 多元微積分
多元微積分沿任何直線 y=kx 趨近於原點 (0,0) 時,f趨近於0。然而,當變數x,y沿拋物線 y=x 趨近於原點時,f趨近於0.5。由於沿不同路逕取極限時函式值不同,故該函式在原點的極限不存在。
每一個變數的連續不是多元函式連續的充分條件:例如, 含有兩個變數的實數函式f(x,y),對於每一個固定的y,f關於x的函式在其定義域內連續。同樣的,對於每一個固定的x,f關於y的函式在其定義域也內連續,但這不能說明原函式連續。
舉一個例子,考慮函式
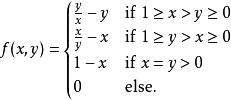 多元微積分
多元微積分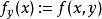 多元微積分
多元微積分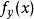 多元微積分
多元微積分 多元微積分
多元微積分 多元微積分
多元微積分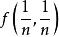 多元微積分
多元微積分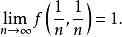 多元微積分
多元微積分很容易驗證,在實數域中,定義函式:,則對於每一個固定的y ,在上連續。同理,函式 也是關於 y 的連續函式。然而,函式f在原點是不連續的。 考慮序列(n為自然數),若在原點連續其結果應為 f(0,0)=0。然而,通過計算知其在原點的極限為。 因此,f在原點不連續。
偏導數
偏導數將導數的概念推廣到更高維度。一個多變數函式的偏導數是一個相對於一個變數的導數,所有其他變數視作常數,保持不變。
 多元微積分
多元微積分偏導數可以組合起來,創造出形式更複雜的導數。在向量分析中,Nabla運算元()依據偏導數被用於定義這些概念:梯度,散度,旋度。在含有偏導數的矩陣中,雅可比矩陣可以用來表示任意維空間之間的函式的導數。因此,導數可理解為從函式定義域到函式值域的逐點變化的線性映射。
含有偏導數的微分方程稱為偏微分方程或“PDE”。這些方程較只含有一個變數的常微分方程更難解出。
重積分
重積分將積分的概念拓展至任意數量的變數。二重積分和三重積分可用於計算平面和空間中區域的面積和體積。富比尼定理給出了使用逐次積分的方法計算二重積分的條件。
可以用曲面積分和曲線積分在曲面和曲線等流形上進行積分。
基本定理
在一元微積分中,微積分基本定理建立了導數與積分的聯繫。多元微積分中導數與積分之間的聯繫,體現為矢量微積分的積分定理:
•梯度定理
•斯托克斯定理
•高斯散度定理
•格林公式.
在對多元微積分更深層次的研究中,可以認為以上四條定理是一個更一般的定理的具體表現,即廣義斯托克斯定理,後者適用於在流形上對微分形式進行積分。
向量分析
 多元微積分
多元微積分向量分析研究歐式空間中足夠光滑的標量和矢量場,即歐式空間E中的一個開集到和 E的可微函式。因此向量分析是多元微積分的一個分支微分幾何里的內容。
 多元微積分
多元微積分不過,向量分析的重要性源自它在物理學和工程科學中的廣泛套用,所以上面的 E常限制為,即通常的三維空間。在這種語境下,矢量場給空間中的每個點賦予一個帶有三個實數分量的矢量,而標量場給每個點賦予一個實數。以湖水為例,湖水各處的溫度形成一標量場,而各處的速度則形成一矢量場。因此,矢量分析是流體力學、氣象學、靜電學、電動力學和地球物理學的基本工具。

