基本介紹
在中學的立體幾何中，有關多邊形內切球和多邊形外接球半徑的計算題目，占有重要的地位，現在來簡述一下這些球的基本性質。
多邊形內切球球心是多邊形一切二面角平分面的交點。
多邊形外接球球心O的位置可用下述方法之一定出來：
1)點O是通過多面體非平行平面外接圓的圓心並垂直於非平行平面的兩條直線的交點；
2)點O是通過多面體非平行棱中點、並垂直於這些棱的三個平面的交點；
3)點O是通過一個面的外接圓圓心，且垂直於此圓的平面∑的直線和垂直於過不與∑平行的棱的中點的平面，且垂直於此棱的直線的交點。
一個球面是由四個非共面的點所確定的。因此，求解多面體外接球半徑的任何習題都可由其內切球的證明和計算繞某個三稜柱外接球的半徑(頂點是給定多面體的頂點)得出來 。
相關結論
長方體一定有外接球，外接球的球心即其體對角線的交點，半徑為體對角線的一半。
正方體既有內切球，也有外接球，球心都是體對角線的交點，內切球的半徑為棱長的一半，外接球的半徑為體對角線的一半。
長方體外接球的直徑=長方體的體對角線長。
正方體外接球的直徑=正方體的體對角線長。
圓柱體外接球的直徑=圓柱體的體對角線長 。
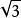外接球正方體的外接球半徑與內接球半徑之比為。
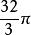外接球【例1】 已知正方體外接球的體積是，那么正方體的棱長等於( )。
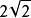外接球
外接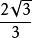球
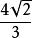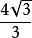外接球
外接球A. B. C. D.
【分析】正方體外接球的直徑為體對角線。
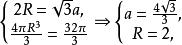外接球【解析】設正方體的棱長為a，外接球半徑為R，則故選D。
【例2】若圓柱體的高增大到原來的2倍，底面積增大到原來的4倍，則其外接球的體
積增大到原來的外接球的體積的倍數是( )．
A．4.5 B．8 C．9 D．16 E．-15
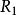外接球【解析】 設原來的圓柱體的底面半徑為r，高為h，外接球的半徑為，
則
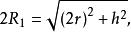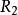外接球
外接球現在的圓柱體的底面半徑為2r，高為2h，外接球的半徑為，則
外接球體積倍數為8。
綜上所述，答案是B。
