核心思想
 威廉‧夏普
威廉‧夏普理性的投資者將選擇並持有有效的投資組合,即那些在給定的風
險水平下使期望回報最大化的投資組合,或那些在給定期望回報率的水平上使風險最小化的投資組合。解釋起來非常簡單,他認為投資者在建立有風險的投資組合時,至少應該要求投資回報達到無風險投資的回報,或者更多。
計算公式
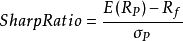 夏普比率
夏普比率其中E(Rp):投資組合預期報酬率
Rf:無風險利率
σp:投資組合的標準差
目的是計算投資組合每承受一單位總風險,會產生多少的超額報酬。比率依據資本市場線(Capital Market Line,CML)的觀念而來,是市場上最常見的衡量比率。當投資組合內的資產皆為風險性資產時,適用夏普比率。夏普指數代表投資人每多承擔一分風險,可以拿到幾分報酬;若為正值,代表基金報酬率高過波動風險;若為負值,代表基金操作風險大過於報酬率。這樣一來,每個投資組合都可以計算Sharpe Ratio,即投資回報與多冒風險的比例,這個比例越高,投資組合越佳。
舉例而言,假如國債的回報是3%,而您的投資組合預期回報是15%,您的投資組合的標準偏差是6%,那么用15%-3%,可以得出12%(代表您超出無風險投資的回報),再用12%/6%=2,代表投資者風險每增長1%,換來的是2%的多餘收益。
夏普理論告訴我們,投資時也要比較風險,儘可能用科學的方法以冒小風險來換大回報。所以說,投資者應該成熟起來,儘量避免一些不值得冒的風險。同時當您在投資時如缺乏投資經驗與研究時間,可以讓真正的專業人士(不是只會賣金融產品給你的SALES)來幫到您建立起適合自己的,可承受風險最小化的投資組合。這些投資組合可以通過Sharpe Ratio來衡量出風險和回報比例。
注意問題
夏普比率在運用中應該注意的問題夏普比率在計算上儘管非常簡單,但在具體運用中仍需要對夏普比率的適用性加以注意:
1、用標準差對收益進行風險調整,其隱含的假設就是所考察的組合構成了投資者投資的全部。因此只有在考慮在眾多的基金中選擇購買某一隻基金時,夏普比率才能夠作為一項重要的依據;
2、使用標準差作為風險指標也被人們認為不很合適的。
3、夏普比率的有效性還依賴於可以以相同的無風險利率借貸的假設;
4、夏普比率沒有基準點,因此其大小本身沒有意義,只有在與其他組合的比較中才有價值;
5、夏普比率是線性的,但在有效前沿上,風險與收益之間的變換並不是線性的。因此,夏普指數在對標準差較大的基金的績效衡量上存在偏誤;
6、夏普比率未考慮組合之間的相關性,因此純粹依據夏普值的大小構建組合存在很大問題;
7、夏普比率與其他很多指標一樣,衡量的是基金的歷史表現,因此並不能簡單地依據基金的歷史表現進行未來操作。
8、計算上,夏普指數同樣存在一個穩定性問題:夏普指數的計算結果與時間跨度和收益計算的時間間隔的選取有關。
儘管夏普比率存在上述諸多限制和問題,但它仍以其計算上的簡便性和不需要過多的假設條件而在實踐中獲得了廣泛的運用。
基金較高的淨值增長率可能是在承受較高風險的情況下取得的,因此僅僅根據淨值增長率來評價基金的業績表現並不全面,衡量基金表現必須兼顧收益和風險兩個方面,夏普比率就是一個可以同時對收益與風險加以綜合考慮的指標。夏普比率又被稱為夏普指數,由諾貝爾獎獲得者威廉·夏普於1966年最早提出,目前已成為國際上用以衡量基金績效表現的最為常用的一個標準化指標。
理論基礎
夏普比率的大小對基金表現加以排序的理論基礎在於,假設投資者可以以無風險利率進行借貸,這樣,通過確定適當的融資比例,高夏普比率的基金總是能夠在同等風險的情況下獲得比低夏普比率的基金高的投資收益。例如,假設有兩個基金A和B,A基金的年平均淨值增長率為20%,標準差為10%,B基金的年平均淨值增長率為15%,標準差為5%,年平均無風險利率為5%,那么,基金A和基金B的夏普比率分別為1.5和2,依據夏普比率基金B的風險調整收益要好於基金A。為了更清楚地對此加以解釋,可以以無風險利率的水平,融入等量的資金(融資比例為1:1),投資於B,那么,B的標準差將會擴大1倍,達到與A相同的水平,但這時B的淨值增長率則等於25%(即2*15%-5%)則要大於A基金。使用月夏普比率及年夏普比率的情況較為常見。