基本介紹
在客觀世界中,各種系統的狀態變化大部分都是連續漸變的,對於這種連續過程的定量理論描述就是微積分和微分方程等數學理論;而自然界中,同樣存在另一類非連續的過程,即突變過程。這種突變現象如何用數學形式來表述,是很值得研究的問題。
1969年法國數學家托姆(R.Thorn)首先提出了突變理論(Catastrophe Theory),並於1975年出版了這方面的一本專著《結構穩定性和性態發生學》。幾乎同時,英國數學家齊曼(E.C.Zeeman)對突變理論也做了許多重要工作,於是突變理論便成了數學中的一個分支。
實質性狀態變數不多於2,余維數不大於4時,可能出現的所有突變類型,托姆稱它們為 初等突變或 基本突變。
k次截斷與k次確定
 基本突變
基本突變一個單變數函式在原點的Taylor級數展開為
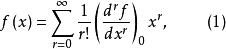 基本突變
基本突變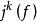 基本突變
基本突變把展開式中k次項以後的項去掉,所剩下的項稱為 k次截斷,用符號表示為
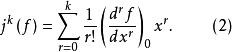 基本突變
基本突變例如,
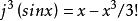 基本突變
基本突變如果一個函式與任何有同樣k次截斷的函式類型相同,則它被稱為 k次確定。上述定義同樣適用於多變數系統 。
突變的基本類型
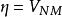 基本突變
基本突變下面討論突變生成函式的拓撲等價形式。首先討論只有一個實質性狀態變數x的情況,因為x為實質性狀態變數,必然有
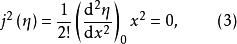 基本突變
基本突變設
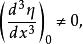 基本突變
基本突變則有
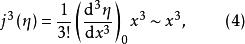 基本突變
基本突變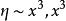 基本突變
基本突變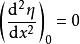 基本突變
基本突變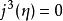 基本突變
基本突變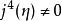 基本突變
基本突變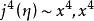 基本突變
基本突變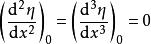 基本突變
基本突變或寫為是摺疊突變生成函式的拓撲等價形式,或稱它為 摺疊突變核。它的余維數為1,因為只有—個方程。如果三次截斷也為零,即,而,則有是 尖點突變核。因為存在兩個方程,它的余維數為2。以此類推,可找到余秩數為1和余維數小於或等於4的其他兩類突變核 。
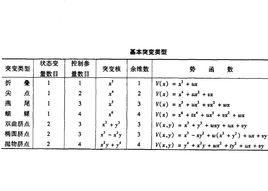
假定一個系統的動力學可以由一個光滑的勢函式導出,托姆用拓撲學的方法證明了:可能出現性質不同的不連續構造的數目並不取決於狀態變數的數目(這可能很大),而取決於控制變數的數目(這可能很小)。按照托姆突變理論分類定理,自然界和社會現象中的大量不連續現象,可由某些特定的幾何形狀來表示。只要控制參量的個數不超過5,那么,按某種意義的等價性分類,總共有11種突變類型。但發生在三維空間和一維時間的四個因子控制下的形形色色的初等突變,概括起來只有7種性質的基本類型,如表1所示。這些數學模型具有高度的概括性和普遍性,其證明是相當困難的,但掌握證明的結果卻是比較容易的 。
| 突變類型 | 狀態變數數目 | 控制參量數目 | 突變核 | 余維數 | 勢 函 數 |
| 折 疊 | 1 | 1 | x | 1 | 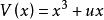 基本突變 基本突變 |
| 尖 點 | 1 | 2 | x | 2 | 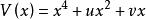 基本突變 基本突變 |
| 燕 尾 | 1 | 3 | x | 3 | 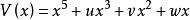 基本突變 基本突變 |
| 蝴 蝶 | 1 | 4 | x | 4 | 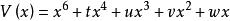 基本突變 基本突變 |
| 雙曲臍點 | 2 | 3 | x+y | 3 | 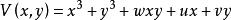 基本突變 基本突變 |
| 橢圓臍點 | 2 | 3 | x-xy | 3 | 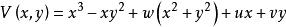 基本突變 基本突變 |
| 拋物臍點 | 2 | 4 | xy +y | 4 | 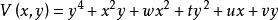 基本突變 基本突變 |