基本介紹
在突變理論中，一個現象(或系統)可以用一個勢函式f來描述，即：
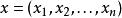突變數學模型
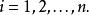突變數學模型1.存在稱為內部空間(或狀態空間)的流形M，M是n維歐氏空間R 內的開集，R 的點x的坐標用表示，x稱為內部變數或狀態變數，
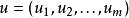突變數學模型
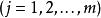突變數學模型2.存在稱為外部空間(或控制空間)的R的開集U，U的點u用坐標表示，u稱為外部變數(或控制變數)或外參數。
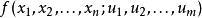突變數學模型
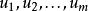突變數學模型
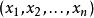突變數學模型3.存在一個勢函式f，它是M×U上的函式，即，對給定的控制參數，系統的狀態應使勢函式f取極小值。
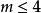突變數學模型
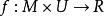突變數學模型
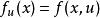突變數學模型在基本突變模型中，，描述現象的勢函式f為一個可微函式，對應於參數u的勢函式f(即)的局部極小值一般確定了現象的一個可能狀態，這一現象的過程則是這些狀態的集合，若現象(系統)發展的規律是由一個依賴於外參數u的狀態空間M上的勢函式所描述，則稱為靜模型。若現象發展的規律是由一個依賴於外參數u的狀態空間M上的向量場所描述，則稱為代謝模型 。
相關說明
突變理論產生於數學和生物學。它的突出特點，是用形象而精確的數學模型來描述自然界連續的漸變是怎樣引起突變的 。
我們已經知道，自然界中存在著兩種基本的演化方式，一種是連續光滑的漸變，另一種是不連續躍遷的突變。單純的漸變演化過程不難見到，而突變沒有漸變相伴則不可能出現。若說有例外的話，那就是居維葉說的由“災變”導致的物種滅絕的突變形式。長期來，由於人們一直不理解連續變化會引起突變的一般機制，因此，把這兩種基本的變化視為不相容的形式。
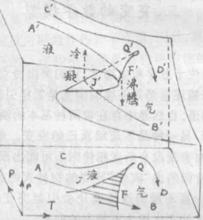圖1 尖點型模型難道自然界不存在漸變與突變統一在一個演化過程的形式嗎?突變理論成功地解決了這個問題。突變理論認為漸變與突變統一在一個形式中的演化方式是自然界中最普遍的方式，突變理論要處理的就是這種極為普遍的演化方式。通過嚴格的推導，托姆證明了一個重要的數學規律：當那些導致突變的連續變化的控制因素不多於四個時，自然界形形色色的突變可以用七種最基本的數學模型來處理。這七種最基本的 突變類型是： 折迭型、 尖點型、 燕尾型、 蝴蝶 型、 雙曲型、 橢圓 型、 拋物型。這些模型具有高度的概括性和普適性。我們從七種突變類型中抽出“尖點型模型”來解剖，適合這個模型的一個典型的例子是物相變化，如氣液相變。在突變理論中，把那些影響相變的連續變化的因素稱為控制變數，把那些代表質變的量稱為狀態變數。在水的相變模型中，控制變數是溫度T和壓強P，它們始終是連續變化的，而狀態變數是水的密度ρ。密度高的狀態相應著液態，密度低的狀態相應著氣態。T、P、ρ不三個變數組成三維行為空間，其水平兩軸表示相變的條件：溫度與壓強，稱為控制平面，垂直的第三軸表示水的狀態：密度。水的密度變化用一特殊的曲面表示，稱為行為曲面。整個曲面由液態高密度區往氣態低密度區傾斜。說明隨著溫度升高及壓強降低，水的密度變小。模型中曲面奇特的地方在於它有一個平滑的折迭曲面。折迭越向後越窄，最後消滅在三層匯合的那一點Q’上。折迭曲面上的點對應著不同的溫度、壓強下水的密度，折迭上葉代表液態，下葉代表氣態。突變理論證明，折迭的上葉和下葉是密度的穩定狀態，中間那一葉是密度的不穩定狀態，折迭區在底平面上的投影為一個小角形區域JOF，它的頂端是尖的，所以這個模型被稱為尖點型。它可以成功地描述溫度和壓強的連續變化，在什麼時候會導致不連續的相變。我們構想溫度和壓強沿AB方向連續變化，在相應的行為曲面上，水的密度沿著曲線A’，F’，B’變化。起初，在A’，F’階段，水的密度在折迭區上時連續下降，表示水密度在漸變，但到了折迭的邊緣F’，溫度壓強只要稍順AB方向離開F點。水密度值就突然跌到曲面下葉的氣態區域，發生不連續變化，這就是沸騰現象。反之，如果溫度和壓強沿著與AB相反的方向變化，可以看到起初氣態密度在曲面下葉沿B’，J’連續地有所增加，但到了折迭的另一個邊緣J'，穩定的行為曲面又中斷了，密度值突然上升到曲面上葉的液態區域，發生了不連續的變化，這就是冷凝現象。十分有趣的是，如果溫度與壓強沿著CD曲線變化。繞過了尖角形的折迭區，相應行為曲面上的點沿著C’D’平滑連續地變化，不出現突變而到達氣態區。這就解釋了為什麼只要溫度與壓強繞過臨界點，水的氣化過程中液態可以不經過沸騰而通過一系列中間密度狀態連續地變為氣體。
這個尖點型模型不是為了說明相變特意設計出來的，它適用於兩種質態能夠可逆地相互轉化的過程。突變理論從數學上證明，當控制量是兩個時，最簡單的突變模型都是這種尖點型的。各種突變中控制變數和狀態變數的物理意義可能不同，但只要符合尖點型的條件，突變都應在尖角形的折迭區發生 。
