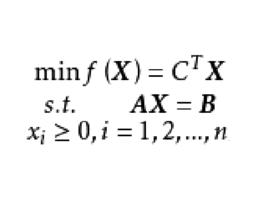基本介紹
線性規劃中的約束條件除變數非負性限制外都採用等式約束, 線性規劃問題的一般形式為
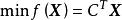 基本可行解
基本可行解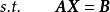 基本可行解
基本可行解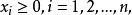 基本可行解
基本可行解式中
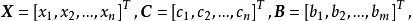 基本可行解
基本可行解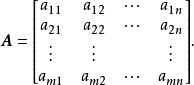 基本可行解
基本可行解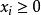 基本可行解
基本可行解AX= B稱為約束方程, A為係數矩陣, B為常數向量,稱為變數非負約束。一般情況下,應有m<n。此時約束方程有無窮多組解。線性規劃就是從這無窮多組解中尋找一組使 目標函式值最小的最優解。
線性規劃問題的 約束條件包括約束方程和變數非負約束兩部分,對應的解也分基本解、基本可行解和最優解。其中 基本解是只滿足約束方程的解; 基本可行解是同時滿足約束方程和變數非負約束的解。基本可行解中能使目標函式值最小的稱為 最優解。
基本解的產生和轉換
約束方程實際上是一個包含n個變數和m個方程的線性方程組,若令變數中的n—m個等於零,求解方程組得到的解稱為線性規劃的基本解。
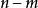 基本可行解
基本可行解在一個基本解中,稱這個為零的變數為非基本變數,稱另外的m個變數為基本變數。
係數矩陣 A和常數向量 B合併組成增廣矩陣:
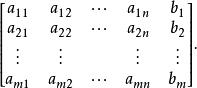 基本可行解
基本可行解對此增廣矩陣進行一系列初等行變換,並進行m次消元,可將上述的增廣矩陣和約束方程變為
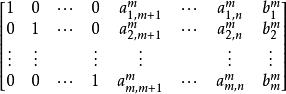 基本可行解
基本可行解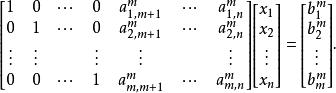 基本可行解
基本可行解由此不難看出,線性規劃問題的一個基本解為
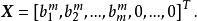 基本可行解
基本可行解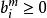 基本可行解
基本可行解若變換後的常數項均為非負值,即,則此基本解也是一個基本可行解。
基本可行解的產生與轉換條件
基本可行解是同時滿足約束方程和變數非負約束的解。
根據線性規劃問題的不同特徵,一個初始基本可行解的獲得可分為下列兩種情況:
(1)如果除變數非負約束之外的約束條件全部是“≤”的不等式約束,而且對應的常數向量中的元素均為正數,此時只要引入鬆弛變數,並以鬆弛變數為基本變數,得到的解自然就是一個基本可行解。
(2)如果除變數非負約束之外的約束條件中還包含等式約束,此時可以在各個等式約束中分別引入一個與鬆弛變數類似的變數,稱為人工變數,然後建立一個輔助規劃問題,求解此輔助規劃問題,就可以得到一個基本可行解。
基本可行解之間的相互轉換採用消元法,轉換時注意以下幾個問題:
(1)變換後所得解的目標函式值必須下降。若下降量最大,此條件稱為 最最佳化條件。
(2)變換後仍然是一個基本可行解,即常數項的值大於等於零,此條件稱為 非負性條件。
(3)最優解的判斷。
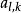 基本可行解
基本可行解滿足上述條件的變換,從根本上說就是要在非基本變數所對應的矩陣元素中找到一個合適的變換主元。
基本可行解轉換的最優性條件
選定主元列的方法可概括為
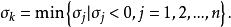 基本可行解
基本可行解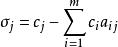 基本可行解
基本可行解 基本可行解
基本可行解式中,稱為第列的判別數。
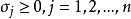 基本可行解
基本可行解如果,對應的基本可行解就是要找的最優解。
基本可行解轉換的非負性條件
按下式選取主元,並進行消元變換:
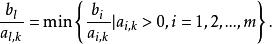 基本可行解
基本可行解這樣,就可以保證變換後的常數項仍為非負,保證由一個基本可行解變換得到的解仍然是一個基本可行解。