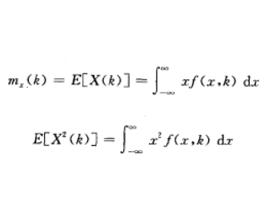基本介紹
數學期望
以實驗中觀查實驗結果值的算術平均為例,解釋數學期望的物理含義:
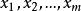 均方值
均方值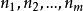 均方值
均方值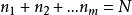 均方值
均方值設共作了N次獨立實驗,實驗結果值為x,x可能有m種值,即,在N次實驗中各x值得到的次數分別為,則有次,故可求出x的算術平均值為:
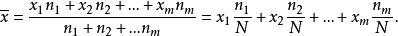 均方值
均方值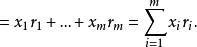 均方值
均方值 均方值
均方值 均方值
均方值根據 大數定理,當時,趨於穩定,即趨向某一機率值,故上述可寫成:
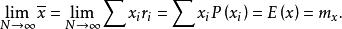 均方值
均方值 均方值
均方值 均方值
均方值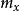 均方值
均方值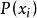 均方值
均方值因為不可能達到的,因此P(x)的確切值是得不到的,E(x)只是一種 期望值(ExpectedValue),故稱為 數學期望。實際上它可看成x的 均值。(值出現的機率) 。
均方值和方差
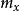 均方值
均方值 均方值
均方值在機率統計中,對於離散型隨機變數其均方值和方差如下(表示的均值):
均方值
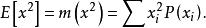 均方值
均方值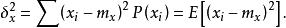 均方值
均方值方 差:
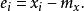 均方值
均方值偏 差:
所以方差也稱為偏差的 均方值。
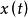 均方值
均方值對於隨時間連續變化的一個變數x(也可看時),其數學期望可寫成:
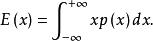 均方值
均方值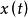 均方值
均方值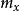 均方值
均方值它實際上就是的平均值。
 均方值
均方值均方值:
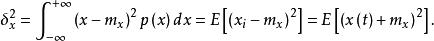 均方值
均方值方差為:
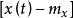 均方值
均方值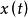 均方值
均方值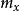 均方值
均方值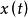 均方值
均方值其中稱為 偏差,為t時刻x變數的取值,為的平均值 。
隨機信號的特性
隨機過程的各個樣本記錄都不一樣,因此不能象確定性信號那樣用明確的數學關係式來表達。但是,這些樣本記錄卻有共同的統計特性,因此,隨機信號可以用機率統計特性來描述。常用的有以下幾個主要的統計函式:
(1) 均方值、均值和方差;
(2) 機率密度函式;
(3) 自相關函式;
(4) 功率譜密度函式;
(5) 聯合統計特性。
均方值、均值和方差
隨機信號的強度,可以用其均方值來描述。對於平穩的遍歷性隨機過程,隨機信號的均方值用樣本函式平方值的時間平均來表示,即
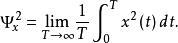 均方值
均方值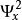 均方值
均方值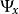 均方值
均方值稱為 均方值,均方值的正平方根稱為 均方根值,表示為。
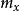 均方值
均方值工程上常把數據信號看成是不隨時間而變化的靜態分量(即直流分量) 和隨時間而變化的動態分量二部分之和。靜態分量可用均值來表示,均值用公式表示
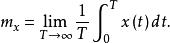 均方值
均方值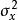 均方值
均方值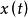 均方值
均方值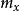 均方值
均方值隨機信號的動態分量部分可以用方差來表述。方差是偏離均值的平方的均值,它反映了過程離開均值的波動情況。用公式表示
 均方值
均方值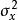 均方值
均方值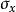 均方值
均方值方差的正平方根為標準偏差,這在誤差分析中是十分重要的參數。展開上式可知方差等於均方值減去均值的平方,即
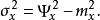 均方值
均方值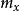 均方值
均方值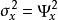 均方值
均方值當均值等於0時,則。