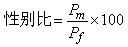正文
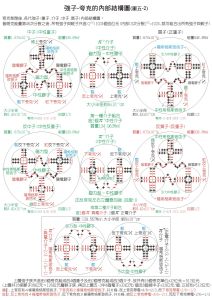原子核-內部結構模型圖 R≈r0A劆用不同的方法定出的常數r0可以略有不同，一般地說，r0＝(1.1～1.5)×10-13 厘米。
從實驗角度看，原子核的核子分布範圍難以直接測量，所以往往用下述兩種相似的概念來代替。一種概念是原子核的電荷分布範圍，即原子核中質子的分布範圍；另一種概念是核力的作用範圍。由於核力是一種短程力，入射強子與核核心子將近接觸時才進入原子核的核力作用範圍，故核力的作用範圍差不多就是核核心子的分布範圍，也就是核物質的分布範圍。
由於原子核沒有明顯的邊界，而只是說核子有一定的空間分布幾率ρN(r)，人們通常以均方根半徑<r2 >┩來描述原子核的大小。對於半徑為R 的均勻球形分布的原子核，其均方根半徑為<r2 >┩＝
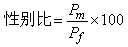。 結合能 要把原子核分解成單個的核子需要給它一定的能量,這個能量叫做原子核的結合能EB。按照A.愛因斯坦的質能關係，原子核的結合能與這個核的質量以及組成它的各個核子質量相聯繫。各個核子的質量和，與它們所組成的原子核的質量之差稱為質量虧損 Δm。質量虧損乘以光速的二次方就等於原子核的結合能，即：
原子核-內部結構模型表 EB(Z,N)＝Δmc2 ＝【Zmp＋Nmn－m(Z,N)】c2 式中mp是質子的質量,mn是中子的質量，m(Z,N)是質子數為Z、中子數為N的原子核的質量,c是光速。EB/A為單位核子的結合能(或稱比結合能)，對於中等質量核及重核，比結合能大致是一個常數（約8兆電子伏）,這樣大的比結合能反映核子之間有很強的吸引力。比結合能大致是一個常數這一事實,與原子中電子的結合能不同,在這方面，原子核很像固體或液體。
把一個粒子 b（質子、中子或其他核子集團）從核內分離出去所需要的最小能量叫粒子b的結合能。
核自鏇 組成原子核的核子是具有自鏇s為啚/2(啚是普朗克常數除以2π) 的粒子，核子在原子核內又具有一定的軌道角動量。各個核子的自鏇和軌道角動量的向量耦合，組成原子核的總動量矩，它就叫核自鏇。核自鏇是用總角動量量子數J 來表示的。J 的數值是啚 的整數或半整數倍。歸納關於基態原子核的實驗結果，人們發現：①偶偶核（即質子數Z和中子數N為偶數的核）的自鏇J 為零，沒有一個例外；②奇奇核的自鏇大多數為不等於零的整數；③奇A核的自鏇J為啚的半整數倍。
原子核的宇稱 宇稱是描述：在空間坐標反演變換(r→-r)下, 量子力學系統波函式變化性質的一個量。例如,描述一個單粒子的波函式,當空間坐標反演時，波函式不變的叫正宇稱（或偶宇稱），波函式改變符號的叫負宇稱（或奇宇稱）。原子核系統的宇稱決定於組成這個系統的各個單粒子的宇稱。原子核的狀態有一定的宇稱，通常用加在自鏇數值右上角的“+”或“-”號來表示，“+”號代表正宇稱，“-”號代有負宇稱。在核過程中，宇稱通常是守恆的；在某些過程中，例如β衰變，宇稱是不守恆的，這是1956年由李政道和楊振寧首先提出，並被實驗所證實的。
磁偶極矩 核磁矩是原子核所具有的一種電磁性質。電荷作軌道運動可以產生磁偶極矩，這個磁偶極矩與軌道角動量成正比。組成原子核的質子帶有正電荷，由於軌道運動，它可對原子核的磁偶極矩有貢獻。核子的自鏇可以引起自鏇磁矩，所以原子核的磁偶極矩等於各核子的自鏇磁矩以及質子的軌道磁矩之和。偶偶核處在基態時，總自鏇為零、磁偶極矩也為零。
原子核的磁矩和核外電子的作用引起核外電子的附加能量，這種附加能量形成原子光譜的超精細結構。
電四極矩 原子核的電四極矩是描述原子核的電荷分布的非球對稱的一個量。（見核四極矩共振）
參考書目
盧希庭主編：《原子核物理》，原子能出版社，北京，1981。
