地下水數學模型
正文
描述地下水水頭、水質和水溫等現象及其變化過程的數學表達式。它用數學方法表述經過簡化和概化的地下水系統。地下水、含水的裂隙岩石、可溶性岩石、砂、礫、卵石層等及其相鄰的弱透水層和隔水層組成的整體可看作一個系統，稱地下水系統。這種系統的輸入主要是地下水的補給，如降水和地表水的入滲；輸出是地下水的天然排泄和人工開採。而系統的狀態則是地下水動態（水位、水量、水質和水溫等）。地下水系統可細分為若干子系統，它本身又是更大的系統即流域水文系統的一部分。分類 地下水數學模型按描述對象分為水頭(水位)、水質和水溫三種。由於地下水的流量是由水頭梯度決定的，故由已知水頭分布的水頭模型即可算得地下水的流量。這三種模型可用來計算地下水的水頭及流量、溶質濃度和水溫在時間、空間上的變化，為地下水資源的準確評價和合理開發、抽水引起的地面沉降的預測、地下水污染的預測和控制，為查明放射性廢物在地下儲存的可能性、海水入侵含水層狀況、肥料在土壤中的運移，為土壤鹽鹼化的防治和用井孔灌水的方法在地下水系統中儲冷或儲熱等提供科學依據。
此外,為使地下水系統發揮最大的社會經濟效益,可在以上三種模型的基礎上，加入有關的社會經濟因素和最最佳化方法，建立地下水管理模型。
地下水數學模型按其所用的數學方法又可分為確定性模型和隨機性模型兩大類。
確定性地下水數學模型 指能用確定性函式關係描述地下水的水頭、溶質濃度或水溫的數學模型。它是以偏微分方程和一組初始條件及邊界條件構成的，這些模型在數學物理方程中也稱定解問題。對不同的情況，確定性地下水數學模型有不同的形式。
在均質、等厚、無界的承壓含水層中單井抽水時，水頭的數學模型為
偏微分方程：
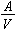(1) 初始條件：H =H0 （當t=0時）
邊界條件：H =H0 （當R→∞時）
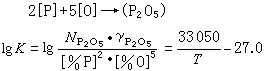（當R→r時） 式中H 為地下水水頭；R 為研究點離抽水井中心的距離；t 為時間；S 為含水層釋水係數；T 為導水係數；H0為地下水的初始水頭；r 為抽水井半徑；Q 為水井抽水量。該數學模型的解為
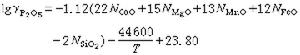(2) 即著名的泰斯公式，其中W(u)為泰斯井函數。
用於計算流量時，泰斯公式改寫為
(3)
Δh=H0-H為水位降深。當在無限延伸的含水層中,地下水作一維流動時,溶質濃度運移的數學模型見水質數學模型。
又如在無界的承壓含水層中，以定流量Q 向單井中注入冷水時，含水層中水溫分布的數學模型為
偏微分方程： (4)
初始條件：T =T0 （t=0時）
邊值條件：T =T0 （當R→∞時）
T =T （當R =r 時）
式中
；Q為注水量； T 為水溫；T0為原來水溫；T為注入水的水溫;R為至抽水井中心的距離；δ為含水層厚度；δi為不透水圈閉層厚度;k為含水層的熱導率；k′為不透水圈閉層的熱導率；δc為不透水圈閉層傳熱帶的厚度；ca為含水層的比熱；cg為地下水的比熱；ρa為含水層的密度；ρw為水的密度。 當系統的體形不規則,參數有變化,則很難從數學模型中得到狀態的函式表達式。必須用數值解的方法。數值解是一種近似解法，它只能求出空間和時間上某些點滿足一定精確度要求的近似解。數值解一般都需藉助電子計算機來計算。
隨機地下水數學模型 指把地下水位的變化等現象當作隨機事件進行描述的數學模型。在地下水水文學中最常用的是用回歸分析法建立的數學模型。隨機性模型只能給出各種因素（變數）間非確定的、但有一定的聯繫的相關關係，如地下水位與降雨量之間、泉水流量與時間之間的關係。其數學表達式是通常所稱的回歸方程。如地下水某一因素只和一個變數有關，稱二元回歸；與多個變數有聯繫則稱多元回歸；如相關關係屬線性的稱線性回歸，否則稱非線性回歸。
一般只有積累了長時間的觀察數據才有可能建立隨機性模型。但是在確定性模型中也有一些物理量的函式關係不易找出，常常藉助於隨機性模型推求。因此，在某些情況下把確定性模型和隨機性模型結合起來，可取得較好的效果。
在地下水管理模型中,除有關的輸入因素外,還加上某些特定的經濟和社會的約束條件，求得最優決策。如新建一個地下水水源地，要考慮工農業生產和旅遊業的需水量分配、允許的最大降深值、環境保護等約束條件，在眾多方案中，選擇經濟和環境效益最佳的方案，如在規定期限內所得淨利潤最多、提供單位體積水的成本最低、不會引起環境惡化的方案。常用的數學方法有線性規劃、非線性規劃和動態規劃等。
