問題分析
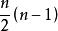 圖的計數
圖的計數問題相當於,對n個無標誌無頂點的完全圖的 條邊,用兩種顏色進行著色,求不同方案數的問題。
比如,兩種顏色x,y,令著上色y的邊從圖中消去,得到一個n個頂點的簡單圖,從母函式形式的polya定理可以得知,不同形的簡單圖形的數目。
下面給出幾個圖的計數問題例子,利用波利亞定理解決。
例1
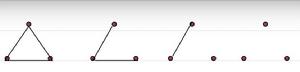
對3個無標誌頂點的完全圖中的邊進行二著色,求不同方案數。
解:完全圖的置換:
–邊隨點動
–不僅僅是旋轉和翻轉
 圖的計數
圖的計數–點的全置換,對應對稱群
對3個頂點來說:
頂點的置換:S3={e,(v1v2v3), (v3v2v1), (v2v3), (v1v3), (v1v2)}
對應邊的置換G={e,(e1e2e3),(e3e2e1),(e1e2), (e1e3),(e2e3)}
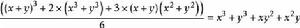 圖的計數
圖的計數P(x,y)=
從P(x,y)可知,對3個頂點的完全圖中的邊著色,其中三條邊都著以色x的一種;同樣兩條邊,或一條邊,或無一條邊著色的x的方案各一種。
例2
4個頂點的圖,對完全圖的邊的2著色,求不同方案數。
解:
S4的每個置換對應6條邊的集上的一個置換
頂點邊 個數
(1)4 (1)6 1個
(1)2(2)(1)2(2)2 6個
(4)1 (2)1(4)1 6個
(2)2 (1)2(2)2 3個
(1) (3) (3)2 2*4個
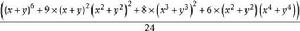 圖的計數
圖的計數P(x,y)=
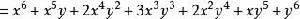 圖的計數
圖的計數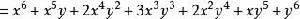 圖的計數
圖的計數=
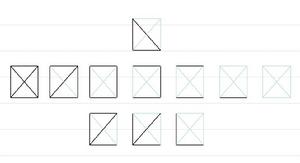 圖的計數
圖的計數例3
求4個頂點的不同構的有向圖的個數。
解:
邊數12條,每個點出邊3條,入邊3條。
頂點置換 有向邊置換
(1)4 (1)12 1個
(1)2(2) (1)2(2)5 6個
(4)1 (4)3 6個
(2)2 (2)6 3個
(1) (3) (3)4 2*4個
P(x,y)= [(x+y)12+6(x+y)2(x2+y2)5 +3(x2+y2)6 +8(x3+y3)4+6(x4+y4)3 ]/24
 圖的計數
圖的計數x2y10的係數為5,所以一共有5個。
