概念
圓環函式(ring function or toroidal function)是圓環坐標系下求解拉普拉斯方程時出現的一類特殊函式,即微分方程:
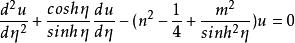 圓環函式
圓環函式的解:
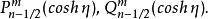 圓環函式
圓環函式它們是連帶勒讓德函式P(z)和Q(z)的特殊情形。圓環坐標系(η,θ,φ)和直角坐標系之間的關係是:
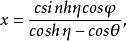 圓環函式
圓環函式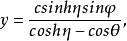 圓環函式
圓環函式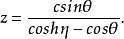 圓環函式
圓環函式拉普拉斯方程
拉普拉斯方程是以法國數學家、天文學家P.S.拉普拉斯(Pierre SimonLaplace)命名的偏微分方程。在電磁學、力學、熱學等學科中,拉普拉斯方程用來描述靜止場(不隨時間變化的場)的特性。令A (x,y,z)是被研究的場量(例如溫度),x、y、z是三維空間直角坐標系的三個坐標量。拉普拉斯方程的具體形式是:
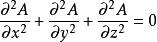 圓環函式
圓環函式採用另一種坐標系,拉普拉斯方程的形式隨之改變。為了擺脫坐標系的具體形式,常將拉普拉斯方程寫成:
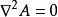 圓環函式
圓環函式靜電場中的拉普拉斯方程三維空間的某個區域Ω中充滿了同一種各向同性的線性電介質,區域Ω內沒有電荷。將Ω中的電位記作V。靜電場的規律由拉普拉斯方程▽V=0描述。
恆定磁場中的拉普拉斯方程區域Ω中充滿了同一種各向同性的線性磁介質,Ω中沒有電流。區域Ω是單連通的。將Ω中的磁標位記作m,恆定磁場的規律由拉普拉斯方程▽m=0描述。
恆定電場中的拉普拉斯方程區域Ω中充滿了同一種各向同性的線性導電體,Ω中沒有電動勢。導電體中的電位V滿足拉普拉斯方程▽V=0。
拉普拉斯方程的解拉普拉斯方程的解,決定於區域Ω邊界上的場量。邊界上給定的場量稱邊界條件。因此,解靜止場的問題,通常是在給定的邊界條件下解拉普拉斯方程:①在區域形狀簡單、邊界條件簡單的條件下,可以用解析方法解拉普拉斯方程。②用實驗方法解拉普拉斯方程,即測量出區域Ω中各處的場量。③利用計算機用數值方法解拉普拉斯方程。隨著計算機技術的發展,數值方法得到廣泛的套用(見電磁場的數值計算)。
泊松方程若▽A=0的等號右端不是0,而是空間坐標的函式,則此方程稱為泊松方程。它是以法國數學家、物理學家S.泊松(S.Poisson)命名的。例如在靜電場的情況下,若區域Ω中有電荷體密度ρ時,電位V滿足泊松方程:
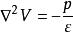 圓環函式
圓環函式其中常數ε為充滿Ω的、同一種各向同性線性電介質的電容率。
微分方程
微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。
微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛,可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題,如空氣的阻力為速度函式的落體運動等問題,很多可以用微分方程求解。此外,微分方程在化學、工程學、經濟學和人口統計等領域都有套用。
數學領域對微分方程的研究著重在幾個不同的面向,但大多數都是關心微分方程的解。只有少數簡單的微分方程可以求得解析解。不過即使沒有找到其解析解,仍然可以確認其解的部分性質。在無法求得解析解時,可以利用數值分析的方式,利用電腦來找到其數值解。動力系統理論強調對於微分方程系統的量化分析,而許多數值方法可以計算微分方程的數值解,且有一定的準確度。
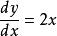 圓環函式
圓環函式含有未知函式的導數,如的方程是微分方程。 一般的凡是表示未知函式、未知函式的導數與自變數之間的關係的方程,叫做微分方程。未知函式是一元函式的,叫常微分方程;未知函式是多元函式的叫做偏微分方程。微分方程有時也簡稱方程。
