圓外切三角形

各邊都和圓相切的三角形叫做圓的外切三角形。 做任意三條切線，然後延長至三條線相交,此三角形則為所求。

定義

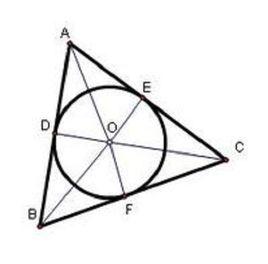
圓外切三角形

在同圓或等圓當中，如果一個三角形的三條邊均與圓相切叫圓外切三角形 。

作法

圓的任意外切三角形的做法：

做圓的任意三條切線，然後分別延長三條切線，直至三條線兩兩相交,此時所得到的三角即為圓的外切三角形 。

性質

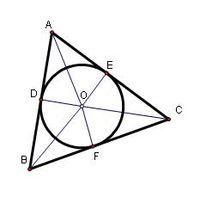圓外切三角形

1、內切圓的圓心到三角形三條邊的距離相等。

如圖：DO=EO=FO

2、內切圓的圓心為三角形三個角的角平分線的交點。

如圖：AO平分∠DAE,BO平分∠DBF,CO平分∠ECF

3、內切圓的圓心與三角形的三邊的連線分別垂直於各切線。

4、如圖：

△DOB≌△FOB；

△FOC≌△EOC；

△DOA≌△EOA。

三角形的內切圓

和三角形各邊都相l刀的圓叫做三角形的內切圓．內切圓的圓心叫做三角形的內心，這個三角形叫做圓的外切三角形 。

關聯：圓的外切三角形所對應的圓為三角形的內切圓。