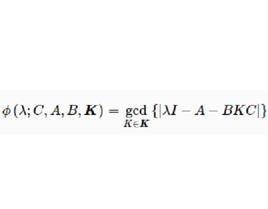定義
考慮一個具有N個局部控制站的大規模線性時不變系統:
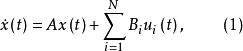 固定模
固定模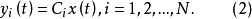 固定模
固定模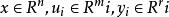 固定模
固定模 固定模
固定模式中:分別表示為系統狀態向量,第控制站的輸入向量和輸出向量。其原始系統的控制和輸出階次為m和 r ,由以下(3)給定
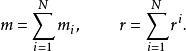 固定模
固定模 固定模
固定模 固定模
固定模和是具有相應階次的實常數矩陣。
分散鎮定問題就是要找出N個具有動態補償器的局部輸出控制規律:
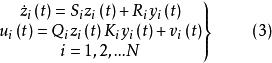 固定模
固定模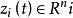 固定模
固定模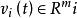 固定模
固定模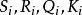 固定模
固定模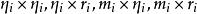 固定模
固定模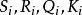 固定模
固定模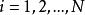 固定模
固定模使整個系統穩定。式中是第 i 個補償器的輸出向量,是 i 控制器外部輸入向量, 矩陣分別為。或者說,分散輸出鎮定是要決定,使得由(1)和(2)所描述的閉環系統其極點在複平面預定的集合之中。
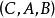 固定模
固定模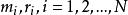 固定模
固定模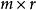 固定模
固定模定義1 考慮由(1)和(2)所描述的系統及整數。令的增益矩陣K代表下述對角方塊矩陣集合中的矩陣:
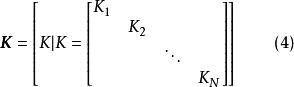 固定模
固定模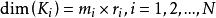 固定模
固定模 固定模
固定模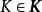 固定模
固定模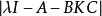 固定模
固定模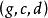 固定模
固定模這裡。那么系統對於 K的“固定多項式”就是對所有,多項式集合的最大公共因子,並用下式表示:
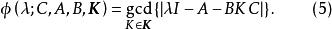 固定模
固定模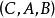 固定模
固定模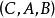 固定模
固定模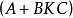 固定模
固定模定義2 對系統和由(4)所給定的輸出反饋的集合,那么對於 K的的 固定模的集合定義為矩陣特徵值所有可能集合的交集,即
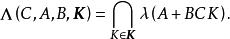 固定模
固定模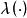 固定模
固定模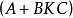 固定模
固定模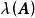 固定模
固定模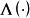 固定模
固定模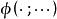 固定模
固定模式中表示特徵值的集合。我們注意到,K可以取零矩陣,因此,固定模的集合包含於。根據定義(1),固定模即是式(5)中固定多項式的根,即
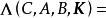 固定模
固定模 固定模
固定模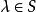 固定模
固定模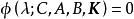 固定模
固定模{|和} (6)
式中S表示在整個S複平面上點的集合。
尋求固定模的方法
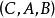 固定模
固定模戴維遜用以下的算法,提供了快速尋求系統固定模的方法。
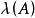 固定模
固定模步驟1 求所有A的特徵值,即。
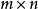 固定模
固定模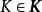 固定模
固定模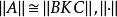 固定模
固定模步驟2 選擇任意矩陣(用偽隨機數發生器或其它方法)使表示矩陣的範數。
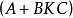 固定模
固定模步驟3 求的特徵值。
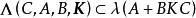 固定模
固定模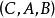 固定模
固定模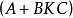 固定模
固定模步驟4 對於 K的,即的固定模包含在與A的特徵值相同的特徵值之中。
步驟5 重複上述步驟4,直到止的固定模完全確定為止。
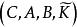 固定模
固定模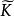 固定模
固定模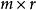 固定模
固定模可以證明:集中系統的固定模,這裡是,即相應於系統不可控和不可觀測的模。
有了固定多項式和固定模的概念之後,就可以導出分散閉環系統穩定的充分和必要條件。
相關定理
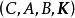 固定模
固定模定理1 對於式(1)和式(2)所描述的系統和式(4)那種類型的對角方決矩陣K, 若且唯若固定模的集合包含在S複平面的左半開平面,即
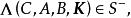 固定模
固定模 固定模
固定模式中表示S複平面的左半開平面,那么式(3)所表示的局部反饋規律才能使系統漸近穩定。