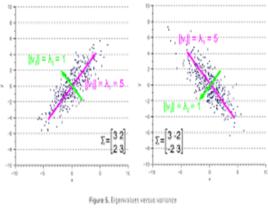
方差旋轉矩陣
方差旋轉矩陣是在乘以一個向量的時候有改變向量的方向但不改變大小的效果並保持了手性的矩陣。旋轉矩陣不包括點反演，點反演可以改變手性，也就是把右手坐標系改變成左手坐標系或反之。所有旋轉加上反演形成了正交矩陣的集合。旋轉可分為主動旋轉與被動旋轉。主動旋轉是指將向量逆時針圍繞旋轉軸所做出的旋轉。被動旋轉是對坐標軸本身進行的逆時針旋轉，它相當於主動旋轉的逆操作。
二維空間
方差最大化旋轉 方差最大化旋轉在二維空間中，旋轉可以用一個單一的角定義。作為約定，正角表示逆時針旋轉。把笛卡爾坐標的列向量關於原點逆時針旋轉的矩陣是：
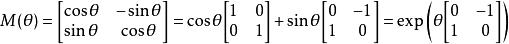方差最大化旋轉三維空間
在三維空間中，旋轉矩陣有一個等於單位1的實特徵值。旋轉矩陣指定關於對應的特徵向量的旋轉(歐拉旋轉定理)。如果旋轉角是 θ，則旋轉矩陣的另外兩個(複數)特徵值是 exp( iθ) 和 exp(- iθ)。從而得出 3 維旋轉的跡數等於 1 + 2 cos(θ)，這可用來快速的計算任何 3 維旋轉的旋轉角。
3 維旋轉矩陣的生成元是三維斜對稱矩陣。因為只需要三個實數來指定 3 維斜對稱矩陣，得出只用三個實數就可以指定一個 3 維旋轉矩陣。
方差最大化旋轉的數學表示
方差最大化旋轉是在主成分分析或因子分析中使用的一種方法，通過坐標變換使各個因子載荷的方差之和最大。 通俗地說，就是：
(a)任何一個變數只在一個因子上有高貢獻率，而在其它因子上的載荷幾乎為0；
(b)任何一個因子只在少數變數上有高載荷,而在其它變數上的載荷幾乎為0.果滿足這個條件的因子載荷矩陣稱為具有“簡單結構”。
方差最大化旋轉就是用來將載荷矩陣旋轉到儘量接近簡單結構的方法。從這組變數代表的樣本看來，方差最大化旋轉找到了一種表示樣本的最簡單的方法，即每個樣本可以用少數變數的函式的線性組合表示。
方差最大化的一種數學表達為：
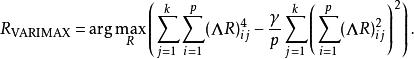方差最大化旋轉這個方法是Henry Felix Kaiser在 1958 提出的，是一種常用的正交旋轉方法（旋轉後各因子仍保持線性不相關）。
