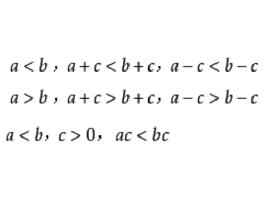基本介紹
不等式 把兩個代數式用不等號(大於“>”,小於“<”,不大於“≤”,不小於“≥”)連線起來所得的式子叫做不等式。
對於任意兩個實數a,b,在a>b,a=b,a<b三種情況之中必須而且只能居一,且:
 嚴格不等式
嚴格不等式嚴格不等式只含有記號“>”或“<”的不等式稱為嚴格不等式。
非嚴格不等式含有記號“≥”或“≤”的不等式稱非嚴格不等式。
不等號左邊的式子叫做不等式的左邊;不等號右邊的式子叫做不等式的右邊。含有字母的不等式,當字母取值使不等式左邊和右邊的值滿足不等號所表示的不等關係時,稱做不等式成立,否則稱做不等式不成立。例如:不論a,b取任何實數值,不等式a +b ≥0一定成立。不論x,y取任何實數值不等式(x+y) <0一定不成立 。
不等式的性質
1.不等式的兩邊都加上(或都減去)同一個數,不等號方向不變。即
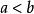 嚴格不等式
嚴格不等式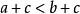 嚴格不等式
嚴格不等式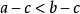 嚴格不等式
嚴格不等式若 ,則 (或 );
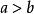 嚴格不等式
嚴格不等式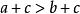 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式若,則(或)。
2.不等式的兩邊都乘以(或都除以)同一個正數,不等號方向不變。即
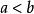 嚴格不等式
嚴格不等式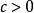 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式若,且,則(或);
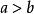 嚴格不等式
嚴格不等式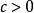 嚴格不等式
嚴格不等式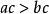 嚴格不等式
嚴格不等式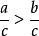 嚴格不等式
嚴格不等式若,且,則(或)。
3.不等式的兩邊都乘以(或都除以)同一個負數,不等號方向改變。即
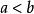 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式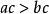 嚴格不等式
嚴格不等式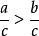 嚴格不等式
嚴格不等式若,且,則(或);
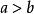 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式若,且,則(或)。
舉例說明:
例如:判斷下列各題正確與否?
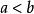 嚴格不等式
嚴格不等式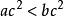 嚴格不等式
嚴格不等式①若,則;
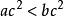 嚴格不等式
嚴格不等式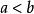 嚴格不等式
嚴格不等式②若,則;
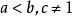 嚴格不等式
嚴格不等式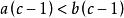 嚴格不等式
嚴格不等式③若,則,。
結論應當是:
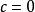 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式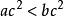 嚴格不等式
嚴格不等式①是錯誤的。因為時,,有,所以不成立;
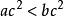 嚴格不等式
嚴格不等式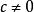 嚴格不等式
嚴格不等式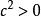 嚴格不等式
嚴格不等式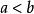 嚴格不等式
嚴格不等式②是正確的。因為由可知,有,所以由性質2可知成立;
 嚴格不等式
嚴格不等式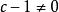 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式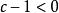 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式③是錯誤的。因為由只能說明,不能確定,當時,,故錯誤 。
相關概念
同向不等式
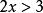 嚴格不等式
嚴格不等式 嚴格不等式
嚴格不等式不等號的方向相同的兩個不等式。如與是同向不等式。
異向不等式
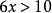 嚴格不等式
嚴格不等式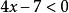 嚴格不等式
嚴格不等式不等號方向相反的兩個不等式。如與是異向不等式 。