抹除碼介紹
抹除碼是相對於複製而言的。使用複製的情況,我們對一個檔案做幾個副本,放在不同的地方,再去管理它們。
抹除碼的思路,簡單來說,是將檔案轉換成一個碎片集合,每一個碎片很小,碎片被打散分布到一組伺服器資源池裡。只要存留的碎片數量足夠,就可以合成為原本的檔案。這可以在保持原本的數據健壯性的基礎上大大減少需要的存儲空間。
概念介紹
原因
在傳統“抹除通道”上的傳輸,通常得仰賴傳送端以及接收端持續性的雙向溝通:首先傳送端的檔案是以多個小數據包的形式進行傳輸的,一個檔案被簡單粗暴地切割成k個數據包大小的片段,傳送端對它們編碼後將這些帶有信息的封包傳送到接收端。這些小的數據包如果在傳輸過程中產生錯誤,就會導致接收失敗,否則就能被成功接收。成功與否取決於接收端在收到每個封包時對其進行的評估,如果該封包可以被解碼,則傳送一個確認(ACK信息)給傳送端;反之,丟棄毀壞的封包,並傳送請求讓傳送端再次傳送該封包。顯然,在這種通道上還會需要一個用於確定哪些數據包需要被重新傳送的反向通道(back channel)。該雙向溝通會持續進行直到所有信息的封包都被成功傳送且解碼為止。
隨著網際網路的迅猛發展,人們在享受信息傳遞的方便與快捷的同時也對通信系統的服務能力和範圍提出了更高的要求,有限的網路頻寬與迅速增長的網路數據量和下載規模之間形成了一對亟需解決的矛盾。網際網路中可靠的數據傳輸一直是許多研究的熱點。很多時候,可靠性是靠使用合適的協定來保證的。例如,普遍使用的TCP/IP用重傳機制來保證傳輸的可靠性。但是在很多情況下,TCP/IP協定並不適用,如點到多點傳輸,或在嚴重損壞的信道上進行傳輸(質量很差的無線或衛星鏈路)。基於反饋重傳的TCP在傳輸距離太長的時候性能很差,因為長距離導致傳送方等待反饋確認信息時的空閒時間太長。同時,單一刪余信道的模型不適用於數據從一個傳送者同時傳送到多個接收者的情況。在這種情況下,從傳送者到多個接收者的刪余信道的刪余機率可能不同。當接收者數量很多時,不太可能估計每個信道的刪余率和丟包情況,因此,需要構造可靠的傳輸方案。
發展歷史
針對這一問題, John Byers及Michael Luby等人於1998年首次提出了數字噴泉(Digital Fountain)的概念,它是針對大規模數據分發和可靠廣播的套用特點而提出的一種理想的解決方案,但當時並未給出實用數字噴泉碼設計方案。2002年,Luby提出了第一種實用數字噴泉碼——LT碼。之後,Shokrollahi又提出了性能更佳的Raptor碼,實現了近乎理想的編解碼性能。在學術理論日漸完善的同時,數字噴泉碼也日益受到產業界的關注,獲得了越來越多的套用[5]。1998年,M. Luby、A. Shokrollahi等人聯合創立了Digital Fountain公司(簡稱DF公司),以推廣數字噴泉概念的實際套用,很快便引起了包括MIT、UC Berkeley、紐約大學、多倫多大學、日本住友電工等機構和單位的關注。目前,已有越來越多的學者和機構開始致力於噴泉編碼的研究,數字噴泉在數據分發與廣播套用上也獲得了越來越多的支持與採納。
基本思想
所謂噴泉碼,是指這種編碼的傳送端隨機編碼,由k個原始分組生成任意數量的編碼分組,源節點在不知道這些數據包是否被成功接收的情況下,持續傳送數據包。而接收端只要收到k(1+ε)個編碼分組的任意子集,即收到一個稍微大於原來k值得N,就可通過解碼以高機率((和ε有關))成功地恢復全部原始分組。
下面這個比喻形象地解釋了這個過程。
單個源節點S如同源源不斷產生水滴(編碼分組)的噴泉,不停地向周圍的多個桶K(表示多個接收端的快取)傳送"水滴"(表示數據包),當一個桶里的水滿了以後(快取滿),它才向源節點傳送一個反饋。每次傳送的水滴是一幀裡面隨機選擇的一些包組合起來的包,這種組合可以是線性的,也可以是非線性的,隨機選擇保證了每次傳送的信息對接收節點是有用的。桶在裝滿水之後(接收足夠數量的水滴),即可達到飲用(成功解碼)的目的,而不必關心具體是哪一滴水(編碼分組)流入桶中。當源節點收到所有桶的ACK以後,再傳送新的一幀,否則繼續傳送組合包。
這也是這種編碼方式被稱為噴泉碼( Fountain Codes)的原因。
特點
精心設計的數字噴泉碼不僅擁有很小的解碼開銷ε,而且具有簡單的編解碼方法和很小的編解碼複雜度。同時噴泉碼還可以有效提高信道容量,使得網路更加健壯。
套用方向
噴泉碼最初是為抹除信道設計的,其最大的特點就是碼率無關性,即編碼器可以生成的編碼符號的個數是無限且靈活的,解碼器只需接收到任意足夠數目的編碼符號就能還原數據。因此不管抹除信道的抹除機率多大,編碼器能源源不斷地產生編碼符號直到解碼器還原出源檔案。正是由於湧泉碼的這個特性,使得湧泉碼在刪除信道中獲得了逼近香農限的性能。
後來,研究發現湧泉碼在二進制對稱信道(BSC)和加性高斯白噪聲(AWGN)等信道中同樣能獲得很好的性能。在此之後,LT碼的研究範圍不斷擴大,LT碼獨特的碼率無關性,特別適合無線通信中的廣播、多播業務,因此LT碼在無線廣播系統和協作中繼網路中的套用成為近幾年的一個研究熱點。
噴泉碼的套用范主要可以概括為如下幾個方面:
①在廣域網、國際網際網路、衛星網上進行高速大檔案傳輸。以RS為代表的前向糾錯編碼通過硬體實現,按照保護小塊數據的要求設計,主要是對受到破壞的多個比特或單個比特進行檢測和校正。而LT碼意在保護大型檔案,而且這種技術以軟體方式實現,速度非常快。由於沒有了TCP的網路時延影響吞吐量,噴泉碼可以在網際網路,無線網,移動網及衛星網上提供接近網路頻寬速度的大檔案傳輸。
②在無線網、移動網提供質量完善的流媒體點播或廣播。利用噴泉碼技術來處理Internet最為頭疼的流式視頻、音頻、視頻遊戲、MP3檔案等,可以提供質量完善的流媒體點播或廣播。
③在3G移動網、數位電視廣播網、電信組播網及衛星廣播系統提供無需反饋信道的可靠性數據廣播。由於不需反饋,用戶數量的增長對於傳送方來說沒有任何影響,傳送方可以服務任意數量的用戶。
兩種噴泉碼
噴泉碼有兩類:LT碼和Raptor碼。LT碼是噴泉碼的第一次具體實現,是由Michael Luby 提出的,後來Amin Shokrollahi對LT碼做出了改進,提出了第二類噴泉碼,即Raptor碼。
1、LT碼(盧比變換碼)
LT碼是第一類碼率不受限碼的實用實現,即其碼率不需要事先確定,同時它具有簡單的編解碼方法以及較小的解碼開銷和編解碼複雜度,為數字噴泉碼的發展奠定了基礎。LT碼是通用的數字噴泉碼,也就是說對於具有不同刪除機率的各種刪除信道均是逼近最優的。
在數據傳輸時,將長為N的檔案分割成k=N/ l個輸入符號(即每個輸入符號的長為l),並稱每個數據包為輸入符號,稱每個編碼包為輸出符號。
定義:LT碼的度分布ρ( d)(d≥1)定義為一個輸出符號結點的度為d的機率。
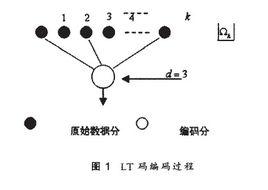
LT碼生成每個編碼分組的過程如圖1所示:
(1)將原始數據等分為k個數據分組,在1~k範圍內按某一分布Ω(稱為編碼度分布)隨機選取一個整數d,其中k稱為該碼的碼長,d稱為編碼分組的度;
(2)在數據分組中均勻地隨機選取d個不同包;
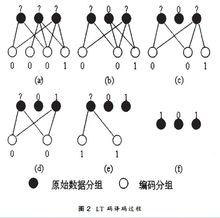
LT碼的解碼採用一種疊代算法[3]。在解碼的每一步,解碼器都在編碼包集合中尋找度為1的包,這些包組成的集合稱為輸出可譯集。它們連線的數據包組成的集合稱為輸入可譯集。顯然,輸出可譯集中的元素與對應的相連的數據包取值相同,因此輸入可譯集中的所有數據包都能被直接譯出。在此之後,解碼器將每一個譯出的數據包與跟它相連的所有編碼包分別進行異或,計算結果取代對應編碼包原來的值,完成之後刪去與它們之間的連線關係。重複上述過程直至不存在度為1的包為止。如果所有數據包都被恢復則解碼成功,否則解碼失敗。該算法即稱為噴泉碼的BP解碼算法。圖2給出了一個解碼實例。其算法過程具體為:
(1)接收一定數量的編碼分組,根據編碼分組間的對應關係(可以通過分組頭部等方式顯式傳遞,也可以通過事先約定偽隨機序列等方式隱式傳遞)建立雙向圖。頂層節點代表原始分組,底層節點代表編碼分組,連線它們的邊代表該原始分組是該編碼分組的模二和分量。簡單實例如圖2(a)所示。
(2)任意選取一個度數為1的編碼分組。如果不存在,則解碼停止;如果存在,則通過簡單的複製運算,即可恢復與之相連的唯一原始分組。簡單實例如圖2(b)所示。
(3)將已經恢復的原始分組模二和到與其相連的所有其他編碼分組中,消除其在這些編碼分組中的模二和分量。相應地,將雙向圖中對應的邊刪除,使得這些編碼分組的度數減1。簡單實例如圖2(c)所示。如果某個編碼分組的度數減小為1,則稱該編碼分組被“釋放”,如圖2(c)最右側的編碼分組。
 噴泉碼
噴泉碼(4)重複步驟(2)和(3),直至解碼停止。如果所有原始分組都已經恢復,則解碼成功;否則,解碼失敗,必須接收更多的編碼分組才能繼續解碼。如圖2(d),2(e),2(f)所示。圖2 LT碼解碼示意
顯然,合理的度數分布是LT碼性能的關鍵。從LT碼編碼過程考慮,一方面應該使平均度數較小,這樣才可以減小生成每個編碼分組需要的運算量;另一方面又應該給予較大度數一定的選取機率,這樣才可以通過m≈k個編碼分組覆蓋所有的原始分組。從LT解碼過程考慮,一方面應該使編碼分組保持一定的釋放速度,這樣才可以保證解碼過程不會終止;另一方面又不能使編碼分組釋放過快,否則大量已經釋放的編碼分組將增加重複覆蓋的可能性,引入不必要的冗餘[7]。正是基於以上考慮,Luby首先給出了理想Soliton分布,使得解碼過程在期望意義下每步疊代恰好釋放一個編碼分組。之後Luby通過修正理想Soliton分布,給出了更加實用的魯棒Soliton分布。理論分析證明:在魯棒Soliton分布下,當受到k+O(k)個編碼分組後,解碼器即可以高機率成功解碼;以模二和運算的次數來衡量,生成每個編碼分組需要的運算量是O(logk),而成功解碼需要的運算量是O(klogk)。根據文獻報告的數據,在Digital Fountain公司設計的商用LT碼中,解碼開銷ε不超過5%,而解碼失敗機率可以低於10-8。可見,LT碼不僅編解碼方法簡單直觀,而且性能相當優良。
2、Raptor碼
Raptor碼是LT碼的基礎上發展出來的改進版。它是基於這樣一個認識:LT碼生成的編碼包中有少量連線度很高的包,這些包的作用主要是保證對所有數據包的良好覆蓋,從而保證解碼的完整性,然而這些高連線度包的存在消耗了很多編解碼異或操作,同時也降低了低連線度包的比例,從而減小了解碼過程中可譯集的大小,降低了解碼成功率。如果能採用別的方法來代替高連線度包完成對數據包的良好覆蓋則可以有效地提高解碼成功率並降低編解碼複雜度。
基於這個思想,Raptor碼提出採用兩步編碼的方式。首先對原始信息用一個分組碼進行預編碼,然後採用一個弱化的LT碼對數據進行編碼並傳送。所謂弱化的LT碼是指它生成的編碼包沒有高連線度包,無法完全譯出原始數據。Raptor碼解碼時,首先用BP算法對數據進行正常解碼。由於弱化LT碼能以很高的機率恢復出絕大多數的數據包,因此剩下未被解碼的數據包所占的比例就被控制在一個很小的範圍以內,這些未被解碼的數據不再通過高連線度的編碼包來保證覆蓋和恢復,而是利用預編碼的糾錯能力進行恢復。通過聯合最佳化弱化LT碼和預編碼的碼率和參數,Raptor可以獲得更低的編解碼複雜度,而在相同解碼開銷下能實現更高的解碼成功率。
Raptor碼的編碼和解碼均需O (kln(1/ε))次包異或操作,其中ε是解碼開銷。可見,Raptor碼的編解碼複雜度與碼長成線性關係,優於LT碼的對數關係。
技術發展
當噴泉碼被用於大規模的多媒體傳輸時,傳統的LT或者Raptor碼無法滿足實時組播套用中的非等重誤碼保護(unequal error protection ,UEP )。Expanding Window Fountain(EWF) codes成為了一種實現這種需求的新方式。顯然,它是一種能夠在抹除信道中的無率(rateless)碼。
EWF碼使用了視窗技術,而不是通過不平等選擇輸入的符號來實現UEP。這種技術通過在UEP無率碼設計中添加附加參數以滿足不同標準的接收者接收,使得它比傳統加權的方式更為一般化並且更具靈活性。無論是理論研究還是實驗表明,這種視窗技術都使得UEP設計具有了更好的性能。