單向方差分析的基本概念
 單向方差分析
單向方差分析單向方差分析又稱單因素方差分析,是最簡單的方差分析方法。所謂的單向(One-Way)就是分析數據中只有一個自變數(又叫因素)。在完全隨機化的(completely randomized)單向方差分析中,有三個方差:總方差(SS)、組間方差(SS)和組內方差(SS,即誤差)。三個方差之間的關係是:。各個方差的計算公式及自由度為:
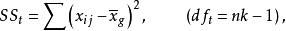 單向方差分析
單向方差分析 單向方差分析
單向方差分析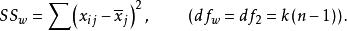 單向方差分析
單向方差分析 單向方差分析
單向方差分析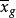 單向方差分析
單向方差分析 單向方差分析
單向方差分析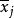 單向方差分析
單向方差分析公式中,n是獨立樣本的容量,k是處理組數,是各個獨立組樣本觀測值的平均數,(g是grand的縮稱)是各個獨立組所有觀測值的平均數,屬第j組第i個數值,是第j組觀測值的平均數。在實際計算中,我們只需求出兩個方差,再根據三個方差之間的數學關係就可以求出另一個方差。它們的均方公式為各自的方差除以各自的自由度:
 單向方差分析
單向方差分析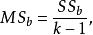 單向方差分析
單向方差分析 單向方差分析
單向方差分析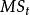 單向方差分析
單向方差分析 單向方差分析
單向方差分析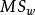 單向方差分析
單向方差分析(代表總均方,代表組間均方,代表組內均方),也可以寫成:
 單向方差分析
單向方差分析 單向方差分析
單向方差分析 單向方差分析
單向方差分析單向方差分析除了要求滿足方差分析的一般條件之外,還要求各組獨立且各觀測值獨立。單向方差分析中,F統計量為組間均方與組內均方(即誤差均方)之比:
 單向方差分析
單向方差分析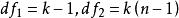 單向方差分析
單向方差分析 單向方差分析
單向方差分析當零假設成立時,F統計量服從自由度為的F分布。F統計量檢驗只能告訴我們在比較的各組(比如三組)平均數中是否至少在兩個組之間有顯著差異性存在,但是不能告訴我們顯著差異性具體表現在哪個或哪些成對組之間。因此,當方差分析發現不同組之間有顯著性差異時,如果想要準確知道顯著性差異的位置,就需要利用事後多重比較(post hoc multiple comparisons)。組間配對比較的次數為。譬如,如果自變數有三個水平,則需要比較的配對數為三對。事後多重比較的方法有多種,下面介紹最為常用的一種方法——Scheffe檢驗(the Scheffe test) 。
Scheffe檢驗
 單向方差分析
單向方差分析Scheffe檢驗可控制整體水平,具有很強的穩健性(robust),也是最為保守的事後比較方法之一。如果兩組數值的平均數差異的絕對值大於Scheffe檢驗臨界值,我們可以認為兩組平均數有統計上的顯著差異存在。相反,如果兩組數值的平均數差異的絕對值小於Scheffe檢驗臨界值,則可以認為兩組平均數沒有統計上的顯著差異。計算Scheffe臨界值的公式為:
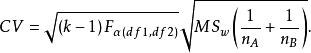 單向方差分析
單向方差分析 單向方差分析
單向方差分析 單向方差分析
單向方差分析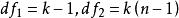 單向方差分析
單向方差分析 單向方差分析
單向方差分析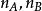 單向方差分析
單向方差分析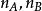 單向方差分析
單向方差分析 單向方差分析
單向方差分析 單向方差分析
單向方差分析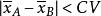 單向方差分析
單向方差分析其中,CV(critical value)代表Scheffe臨界值,k是處理組數(自變數的組數或水平),是在水平上來自自由度為(如果各組樣本容量不等,則的F分布的一個值,MS代表組內均方差,分別表示比較的兩個獨立樣本的容量(如果樣本容量相等,可用n代替),是Seheffe法平均數標準誤差,與各獨立樣本容量的大小有關。當各組樣本容量相等時,各配對比較的樣本平均數的標準誤差相等。當時,可以斷定A和B兩組的平均數有顯著性差異。相反,如果,則認為A和B兩組的平均數沒有顯著性差異 。
套用舉例
為了計算的方便,下面的例子採用小樣本。在實際研究中,要採用更大的樣本,並要在SPSS統計中對樣本進行方差齊性檢驗 。
某高校英語教師對理科、文科和英語專業各10名大學一年級學生進行了聽力水平測試(滿分為20分),成績如下:
文科組(組1)聽力成績:13 12 15 13 12 11 10 8 7 5
理科組(組2)聽力成績:17 16 15 14 14 11 13 12 10 8
英專組(組3)聽力成績:16 18 12 15 13 10 16 15 17 18
試問:三個不同專業的學生聽力成績是否有顯著的差異?
本題涉及三個不同類型組在同一個連續性因變數(聽力成績)方面的比較,符合單向方差分析的條件。
 單向方差分析
單向方差分析【解】已知:n=10,k=3。根據原數據求得:將結果代入公式,求得
 單向方差分析
單向方差分析 單向方差分析
單向方差分析根據F統計量公式,求得
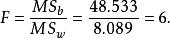 單向方差分析
單向方差分析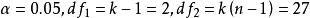 單向方差分析
單向方差分析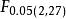 單向方差分析
單向方差分析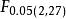 單向方差分析
單向方差分析根據,查F分布表,得到臨界值=3.35。統計量F=6>=3.35,所以p<0.05,拒絕零假設,即認為三個組之間有顯著的差異。
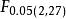 單向方差分析
單向方差分析本題中各獨立樣本的容量相等,所以各組配對比較時的Scheffe臨界值相等。我們知道n=10,k=3,=3.35,MS=8.089,據此求得Scheffe臨界值:
 單向方差分析
單向方差分析 單向方差分析
單向方差分析 單向方差分析
單向方差分析本例中需要比較的三組平均數差異的絕對值分別是:。只有組1和組3平均值差異(組3高於組1)有顯著性意義,由此可以得出結論:英專學生的聽力成績明顯好於文科學生,但是與理科學生沒有顯著差異;文科學生與理科學生的聽力成績沒有顯著差異 。

