概念的提出
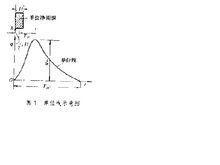單位線示意圖單位線的概念首先是由謝爾曼(L.K.Sherman)於1932年提出。 認為給定流域的地面徑流 (直接徑流) 過程線的形狀反映了該流域所有物理特徵的影響; 它包括三個基本假定， 如在給定時段內和流域面積上淨雨量分布均勻。 單位線的基本假定為： ①單位時段內淨雨量不同， 但所形成的地面徑流過程線的總歷時(即底寬)不變;②單位時段內n倍單位淨雨量所形成的出流過程，其流量值為單位線的n倍; ③各單位時段淨雨所產生的出流過程不相干擾， 出口斷面的流量等於各單位時段淨雨所形成的流量之和， 概言之， 上述單位線概念和假定， 就是將流域視為集總的線性時不變系統， 適用倍比和迭加原則。
單位線是一種由淨雨過程推求洪水過程的方法，在設計洪水和水文預報中廣泛套用。在水文史上占有重要地位。控制單位線形狀特徵的主要指標有：洪峰流量（qm）、洪峰滯時（Tp）和總歷時 T，合稱單位線三要素。圖中坐標 h為淨雨， q為流量， t為時間、△ t為單位時段。
特點及套用
特點
單位線方法簡單易行，效果較好，在洪水預報中套用較廣。但由於單位線的基本假定與實際情況並不完全相符，降雨的時空分布不均，非線性影響和基流分割誤差，使各次洪水所分析的單位線不同，或者出現跳動現象，宜加約束條件或考慮非線性改正。20世紀50年代初期， 中國提出單位線峰值和單位線滯時分別與淨雨量建立非線性的經驗公式，或簡單地依淨雨量大小採用分級單位線，對於暴雨地區分布不同則採用分區的單位線。單位線的時段轉換，可套用S—過程線(它是單位線流量的累積曲線)，將兩條相同的S—曲線沿時間坐標軸按所需時段平移錯開，兩曲線間縱標之差乘以時段換算係數，就得所需要的時段單位線。
套用
流域上單位徑流所形成的出流流量過程線。單位徑流在單位時間內產生單位徑流深。它在流域面上及時段內都應當是均勻分布的。如果徑流是地面徑流，則形成的是地面徑流單位線。地下徑流則形成地下徑流單位線。
假定流域匯流系統是線性的，即每單位徑流所形成的流量過程線之間互不干擾，總流量是各單位徑流所形成的流量的代數和，則已知單位線以後，就可把任何徑流過程所產生的流量過程推算出來。
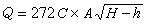公式取單位時距為Δ t，按Δ t間距取值，得單位線過程為 q1， q2,..., q n,徑流過程為 R1, R2,公式
R3,...,出口斷面的流量過程為 Q1, Q2, Q3,...。則在時段 t末的流量 Q t可以公式表示為：
式中 n為單位線時段數。據此式可推算出流域出口的流量過程。
如已知出流流量過程與徑流過程，則根據上式可以反推出單位線。這就是實用上推求單位線的辦法。
單位線從1932年L.R.K.謝爾曼提出以來，套用廣泛，效果顯著。根據現代的線性系統理論，可以把單位線定義為線性系統的單位脈衝反應，即對系統輸入一個脈衝所造成的輸出過程。一個脈衝就是在時距為無窮小情況下輸入一個單位量，單位量無因次。脈衝反應也稱瞬時單位線,要用微分形式表示。在一定條件下,瞬時單位線具有函式形式，例如J.E.納什的瞬時單位線公式為：
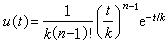公式式中 t為時間; n為階數，也就是串聯線性水庫的個數； k為一個線性水庫的蓄泄係數。
上面假定流域匯流系統是線性的，即在任何情況下單位線不變，解題十分方便。實際上，當徑流的面分布均勻，洪水較大時，上述條件基本符合，單位線的套用效果很好。
線性系統理論已較成熟，單位線的套用技術已有較大的發展。例如可以處理有多個輸入與多條單位線的系統，可以用系統識別方法及時計算出單位線以用於實時預報等。但如匯流系統是非線性的,單位線就要變化,上述公式就不能套用。
細胞生物學 定義
單位線：Bak等（1977）從人胎兒離體培養分裂細胞中分離出染色體，經溫和處理後，在電鏡下看到直徑0.4μm，長11~60μm的染色線，稱為單位線（unit fiber）。
