定義
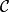 單位態射
單位態射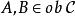 單位態射
單位態射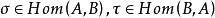 單位態射
單位態射設是範疇,,如有,使得
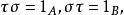 單位態射
單位態射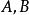 單位態射
單位態射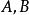 單位態射
單位態射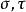 單位態射
單位態射則稱等價(或同構)。滿足上述條件的叫做 單位態射(或 同構態射)。
相關概念
等價態射
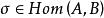 單位態射
單位態射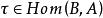 單位態射
單位態射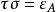 單位態射
單位態射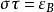 單位態射
單位態射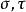 單位態射
單位態射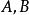 單位態射
單位態射等價態射(equivalent morphism)亦稱 同構態射,它是群論、環論、模論中同構概念的推廣,因此也簡稱同構。在範疇中可用它們將其對象類分成等價類進行研究,因此起著重要的作用,設C為範疇, ,若有 使 且 (ε表恆等態射),則 都稱為 等價態射且互稱為逆態射,此時稱對象 為等價的。 等價態射一定是單位態射 ,反之亦然。等價態射之逆是惟一的 。
單態射
 單位態射
單位態射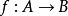 單位態射
單位態射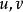 單位態射
單位態射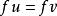 單位態射
單位態射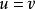 單位態射
單位態射 單位態射
單位態射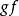 單位態射
單位態射 單位態射
單位態射單態射是集合範疇 中單射概念的推廣,它與滿態射是互為對偶的概念。範疇C中的態射 ,若有左可消性質,即對使態射合成有意義的態射 ,由 可斷定 ,則稱 為C中的 單態射,若 為單態射,則 必為單態射;單態射的合成仍為單態射; 單位態射必為單態射; 甚至左可逆態射也是單態射。
滿態射
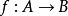 單位態射
單位態射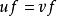 單位態射
單位態射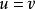 單位態射
單位態射 單位態射
單位態射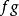 單位態射
單位態射 單位態射
單位態射滿態射是集合範疇中滿射概念的推廣,它是單態射的對偶概念。範疇C中的態射 ,若有右可消性質,即由態射合成 可斷定 ,則稱 為C中的滿態射,若 為滿態射,則 為滿態射;滿態射的合成仍為滿態射; 單位態射必是滿態射,甚至右可逆態射也是滿態射。在群範疇中滿態射即滿同態;在環範疇中滿同態為滿態射,但反之不真。
雙態射
雙態射是集合範疇中雙射概念的推廣,在範疇中同時為單態射與滿態射的態射稱為 雙態射。換言之,雙態射即滿足左可消與右可消的態射,在群範疇與阿貝爾群範疇等範疇中,雙態射就是滿單同態(同構)。 單位態射一定是雙態射, 但反之一般不真 ,在阿貝爾範疇中雙態射即單位態射 。
阿貝爾範疇
阿貝爾範疇(Abelian category)是一種特殊的加性範疇,因此具有更豐富的性質。一個加性範疇C稱C為阿貝爾範疇,若再滿足下述三條件:
1.任何態射f都有核kerf與上核coker f;
2.任何單(滿)態射都是其上核(核)的核(上核);
3.任何態射σ都可分解為一個單態射η與一個滿態射π的合成σ=ηπ(稱為σ的標準分解式)。
阿貝爾群範疇、環R上的R模範疇都是阿貝爾範疇,阿貝爾範疇具有加性範疇的一切性質,阿貝爾範疇的對偶範疇仍為阿貝爾範疇, 阿貝爾範疇中既單且滿的態射是單位態射,阿貝爾範疇在同調代數及代數幾何中都是最常用的一類範疇 。
態射的核
態射的核(kernel of a morphism)是群論中同態核概念的推廣(不過在群論中同態核是一個正規子群,而在群範疇中則是指此正規子群及其在群中的嵌入同態),態射的核是態射的上核之對偶概念。設範疇C有零對象(因而有零態射0),f∈Hom(A,B),所謂f的核ker f,是指C的一個對象K與一個態射η∈Hom(K,A)組成的對(K,η),它滿足:1.η為單態射;2.fη=0;3.對任何g∈Hom(D,A),只要fg=0就必有τ∈Hom(D,K)使ητ=g (條件1可去掉,但在3中須強調“必有惟一的τ”)。
若f的核存在,則在等價意義下是惟一的,有時為強調態射也可不提K而稱η為f的核,因此, 單態射的核是零態射0,零態射的核是單位態射。
態射的上核
態射的上核(cokernel of a morphism)是群論中同態的上核概念的推廣(不過,在群論中同態的上核是指一個商群,而在群範疇中是指此商群及群到此商群的滿同態),態射的上核是態射的核的對偶概念。設範疇C有零對象(因而有零態射0),f∈Hom(A,B),所謂f的上核coker f,是指C的一個對象W與一個態射π∈Hom(B,W)組成的對(W,π),它滿足:1.π是滿態射;2.πf=0;3.對任何的g∈Hom(B,C),只要gf=0就必有τ∈Hom(W,C)使τπ=g (條件1可去掉,但在條件3中須強調“必有惟一的τ”)。
在等價意義下,f的上核如存在必惟一.,有時為強調態射也可不提W而稱π為f的上核,且記為coker f=π,因此,滿態射的上核是零態射0, 零態射的上核是單位態射 。

