定義
商集是集合論的基本概念之一,指由集合和該集合上的等價關係導出的集合。設~是非空集合A的一個等價關係,若把以A關於~的全部等價類作為元素組成一個新的集合B,則把集合B叫做A關於~的商集合,簡稱為商集.記作B=A/~.
特點
非空集合S關於它上面的任何等價關係R的商集具有下列特點:
S/R ≠ ∅;
若A∈S/R,則A ≠ ∅;
若A,B∈S/R,A≠B,則A∩B = ∅.
1.S/R ≠ ∅;
2.若A∈S/R,則A ≠ ∅;
3.若A,B∈S/R,A≠B,則A∩B = ∅.
利用選擇公理,在S/R的每個元素A中取出一個元素a∈A,稱為等價類A的代表,而{a}稱為 商集的代表集。集S對它上面的不同的等價關係R和G有不同的商集,且滿足:
1.S/R=S/R;
2.S/E={{a}},這裡E是恆等關係;
3.S/(S×S)={S}, 這裡S×S是全域關係;
4.若S/R={A},S/G={B},則
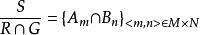 商集
商集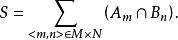 商集
商集且 其中某些項可能是空集。
舉例
例1 A={a,b,c,d,e,f}={某大學宿舍的大學生};R是A上的同鄉關係(不難證明同鄉關係是等價關係),若a,b是北京人,c是廣東人,d,e,f南京人,則R={(a,a)(a,b)(b,a)(b,b)(c,c)(d,d)(d,e)(d,f)(e,d)(e,e)(e,f)(f,d)(f,e)(f,f)}.A中各元素關於R的等價類分別是:
[a]=[b]={a,b};
[c]={c};
[d]=[e]=[f]={d,e,f};
A關於R的商集A/R={[a]R,[c]R,[d]R}={{a,b},{c},{d,e,f}}.
例2 A={(x,y) |-∞<x<+∞,-∞<y<+∞,xy≠0}是除去坐標軸的平面。可以驗證,~={ [(x1,y),(x,y)] | x1x2>0,y1y2>0,(x1,y)∈A,(x2,y2)∈A}是A的等價關係,A關於~的等價類為A= [(1,1)],A= [ (-1,1)],A= [ (-1,-1)],A=[(1,-1)],顯然A,A,A,A就是直角坐標平面上的四個象限(如下圖)。這時A關於~的商集為:A/~= {A,A,A,A}.
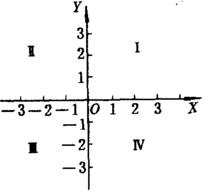 直角坐標平面
直角坐標平面賦范線性空間的商空間
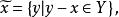 商集
商集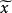 商集
商集設X是線性空間,Y是X的一個線性子空間。對x∈X,記 稱 是以x為代表元的等價類,於是得到 商集
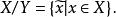 商集
商集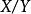 商集
商集在 中規定
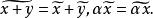 商集
商集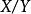 商集
商集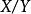 商集
商集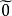 商集
商集易知這樣的線性運算是一意確定的,於是, 按這個線性運算稱為線性空間。在商空間 中,X的子空間Y被“縮”為零向量 .
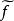 商集
商集例如,在L 空間中,記Y為幾乎處處等於零的函式全體,則對f∈L , 就是與F幾乎處處相等的函式組成的等價類。
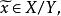 商集
商集如果X為賦范線性空間,Y是X的線性閉子空間,對 規定
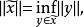 商集
商集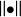 商集
商集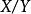 商集
商集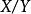 商集
商集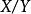 商集
商集容易證明這樣定義的 是上的範數,即仍是賦范線性空間,而且,當X是Banach空間時,商空間也是Banach空間。
附錄
[ 二元關係]設A,B是集合,R是笛卡兒乘積AxB的子集,則稱R是A到B的一個二元關係,例如A={x,y},B={a,b},R={(x,a),(x,b),(y,a),(y,b)}.
[ 自反的二元關係]如果對於集合A的每一個元素a,都有(a,a)屬於二元關係R,則稱R為自反的二元關係。
[ 對稱的二元關係]如果每當(a,b)屬於R,就一定有(b,a)屬於R,則稱R是對稱的二元關係。
[ 傳遞的二元關係]如果每當有(a,b)、(b,c)均屬於R,必有(a,c)屬於R,則稱傳遞的二元關係。
[ 等價關係]R是A上的[二元關係],如果R是自反的、對稱的、傳遞的二元關係,則稱R為A上的等價關係。
[ 等價類]設R是A的等價關係,a是A中的任意元素,由A中的所有與a相關的元素組成的集合,稱為a關於R的等價類。
