定義
 哈納克不等式
哈納克不等式設 是區域Ω中一個非負調和函式,則對Ω的任一緊子集Ω′,存在一個只依賴於n,Ω′和Ω的常數C,使得
 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式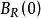 哈納克不等式
哈納克不等式特別地,如果 在以原點為中心,R為半徑的球 中是一個非負調和函式,那么 哈納克不等式有如下形式:
 哈納克不等式
哈納克不等式哈納克原理
泊松公式使我們可以將一個調和函式用它在一個圓周上的值來表示,為了適應目前的需要,我們把它寫成形式
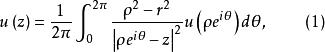 哈納克不等式
哈納克不等式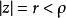 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式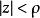 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式其中而假定在中調和(或對調和,對連續)。聯繫初等不等式
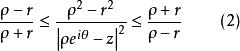 哈納克不等式
哈納克不等式的右端,公式(1)給出估計
 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式如果已知,那么也可用(2)的第一個不等式,得到一個雙重估計
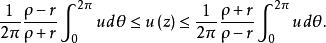 哈納克不等式
哈納克不等式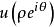 哈納克不等式
哈納克不等式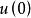 哈納克不等式
哈納克不等式但的算術平均等於,於是最後得到下面的上界與下界:
 哈納克不等式
哈納克不等式這是 哈納克不等式,我們要著重指出,它僅對正的調和函式為真。(3)的主要套用是用於正項級數,或等價地,用於調和函式的增序列。它引出一個強大而簡單的定理,稱為哈納克原理 。
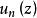 哈納克不等式
哈納克不等式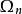 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式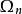 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式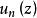 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式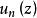 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式哈納克原理:考察函式 的一個序列,其中每個函式定義在某一城 內,且在該域內調和。設 為這樣的一個域,它的每一點具有一個鄰域包含於除有窮個以外的所有 中,並設在這一鄰域中,當n足夠大時,有 。那么這裡只有兩種可能:或者是 在 的每個緊緻子集上一致地趨於 ,或者是 在緊緻集上一致收斂於 內的一個調和極限函式 。
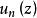 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式最簡單的情形是函式 在 內均為調和,並組成一個非降序列。不過,有很多套用說明這種情形不夠普遍。
 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式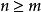 哈納克不等式
哈納克不等式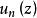 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式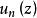 哈納克不等式
哈納克不等式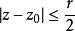 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式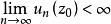 哈納克不等式
哈納克不等式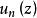 哈納克不等式
哈納克不等式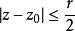 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式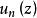 哈納克不等式
哈納克不等式為了證明這一定理,先設至少對於一點 。根據假設,可以找到一個r和m,使得對於 及 ,函式 都是調和的,並組成一個非降序列,如果將不等式(3)的左邊套用於非負函式 ,則知 將在圓盤 中一致地趨於 ,另一方面,如果 ,套用不等式的右邊同樣可證明 在 上有界。因此,在其上 分別為有窮及無窮的兩個集都是開集,而由於 是連通的,故必有一個集是空集。只要 的極限在單一點上是無窮大,則它必恆等於無窮大。至於一致性,可用海涅一博雷爾引理來證明。
 哈納克不等式
哈納克不等式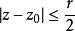 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式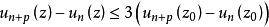 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式在相反的情形,極限函式 是到處均為有窮的,我們現在只要證明其收斂是一致的即可。套用上面的同樣記法,對於 及 ,有 ,因此,在 點收斂就意味著在 的一個鄰域中一致收斂,再套用海涅-博雷爾引理可知在每個緊緻集上收斂是一致的。至於極限函式的調和性,則可從 能用泊松公式來表示這一點而得證。
 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式 哈納克不等式
哈納克不等式設E是包含於域中的一個緊緻集,證明,存在一個只依賴於E及的常數M,使得中的每個正調和函式,對於任意兩點,滿足不等式。

