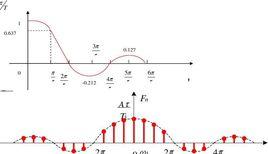
卷積計算
作為理論研究,我們需要周期信號,但在實驗、生產和科研實踐過程中,任何實驗儀器、設備中的周期信號實際上並不是數學上的周期信號,而是因果周期信號,即信號只有單向的周期重複性。因果周期信號是實際設備儀器中的“周期”信號,任何系統在因果周期信號激勵下的0狀態回響又等於因果周期信號與系統單位衝激回響的卷積,因而討論因果周期信號卷積計算方法就有一定的理論和套用價值。
因果周期信號卷積計算在信號與線性系統分析實驗設備中有重要套用,但現行信號與線性系統分析沒有因果周期信號卷積計算方法的深入討論。在做信號與線性系統分析課程的卷積硬體實驗時發現示波器螢幕輸出的因果周期信號自卷積結果是等幅因果周期信號。因果周期信號自卷積結果是漸升因果信號,在有限時段上的卷積結果僅由有限多個單位階躍信號乘指數函式疊加組成 。
信號分析
線性系統分析的重要理論基礎是疊加原理,依據疊加原理可以得出結論:線性系統在任意給定輸入信號f(t)激勵下的零狀態回響y(t),可以用單位衝激信號δ(t)激勵下的零狀態回響h(t),與輸入信號f(t)的卷積給出。這表明,在時域內,卷積積分是求解線性非時變系統零狀態回響的重要方法。直接求解系統單位衝激回響h(t)再作卷積計算總是比直接求解系統零狀態回響y(t)要容易得多。
先給出無窮長因果周期信號卷積計算所需的理論基礎,導出整數階漸升(gradually increased)信號(函式)卷積計算公式,結合數學物理方法中的級數乘法公式,導出因果周期信號卷積計算公式,並在此基礎上快速計算導出因果周期鋸齒波自卷積計算公式,並編程可視化,直觀了解因果周期信號卷積結果信號的時域特徵。
因果周期方波信號激勵下的動態電路零狀態回響可用拉普拉斯積分變換法求解,其難點是由像函式求時域解函式時,要計算像函式乘e唯無窮多個奇點處的留數,計算量較大。因果周期方波信號激勵下的動態電路零狀態回響可在時域中直接求解 。
因果信號與系統
一個信號系統應該有輸入信號和輸出信號,如果輸出信號僅僅與輸入信號的現在時刻或過去時刻有關,則稱該系統為因果系統,輸出輸入信號為因果信號,否則為非因果系統,非因果信號。
因果系統,稱一個系統是“因果”的,是指此系統滿足因果性。因果系統是指若且唯若輸入信號激勵系統時,才會出現輸出(回響)的系統。即因果系統的(回響)不會出現在輸入信號激勵系統的以前時刻;也就是說系統的輸出僅與當前與過去的輸入有關,而與將來的輸入無關的系統。因此,因果系統是“物理可實現的” 。
系統函式H(z)可以表示為H(z)=Y(z)/X(z),即輸出信號的Z變換與輸入信號的Z變換的比值。 如果輸入序列是一個單位衝擊函式x(k)=δ(k),則x(k)的Z變換X(z)=1。將其帶入H(z)的表達式得到Y(z)=H(z),這說明如果輸入是一個單位衝擊序列,則輸出信號的Z變換就是H(z),這就是為什麼H(z)叫做單位衝擊回響的原因。當輸入是單位衝擊時,輸出信號y(k)的Z變換Y(z)的極點就是H(z)的極點。