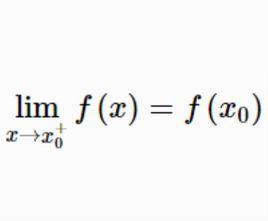基本介紹
由函式f(x)在點x左極限與右極限的定義，立即得到函式f(x)在點x左連續與右連續的定義。
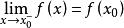右連續如果 ，則稱函式y=f(x)在點x 左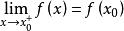連續；
右連續如果 ，則稱函式y=f(x)在點x 右連續。
由極限的充分必要條件易得：函式f(x)在 點x連續的充分必要條件是：函式f(x)在點x既左連續，又右連續，即
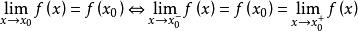右連續函式在一點連續的定義，很自然地可以推廣到一個區間上。
如果f(x)在區間I上的每一點處都連續，就稱f(x)在I上連續，並稱f(x)為I上的連續函式；若I包含端點，那么f(x)在左端點連續是指右連續，在右端點連續是指左連續。
由極限的運算法則可知，常值函式f(x)=C(C為常數)在實數軸上任意一點x都是連續的，多項式函式f(x)在(-∞，+∞)上是連續的，即
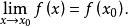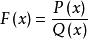右連續
右連續有理分式函式 在分母Q(x)≠0的點是連續的，即有理分式函式在定義域內是連續的 。
例題解析
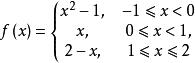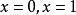右連續
右連續【例1】討論函式在點處的連續性。
解 在x=0處，f(x)有定義，且f(0)=0，
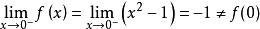右連續因為，所以f(x)在x=0處左不連續；
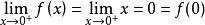右連續因為，所以f(x)在x=0處右連續。
因此，根據上述函式y=f(x)在點x處連續的充要條件知，函式f(x)在x=0處不連續。
在x=1處，f(x)有定義，且f(1)=1，
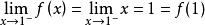右連續因為，所以f(x)在x=1處左連續；
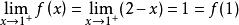右連續因為，所以f(x)在x=1處右連續。
因此，根據上述函式y=f(x)在點x處連續的充要條件知，函式f(x)在x=1處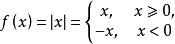連續 。
右連續【例2】證明 在x=0點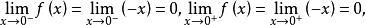連續。
右連續證明 又f(0) =0，
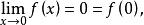右連續故f(x)=|x|在x=0點連續 。
