概念
可分對策(separable game)是一類特殊的無限對策。其贏得函式(亦稱可分函式)為:
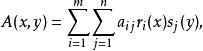 可分對策
可分對策式中a是常數,r(x)和s(y)是連續函式(i=1,2,…,m;j=1,2,…,n).當局中人Ⅰ期望支付的最小值等於局中人Ⅱ期望支付的最大值時,即:
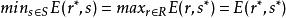 可分對策
可分對策(式中r*=(r*,r*,…,r*)∈R,s*=(s*,s*,…,s*)∈S)時,則稱這樣的策略分別是局中人Ⅰ和Ⅱ在可分對策中的最優策略。稱這樣的值E(r*,s*)為可分對策的最優值。
對策論
運籌學的一個分支,它通過對競爭活動或鬥爭局勢的模型(即對策),加以描述和研究,為競爭或鬥爭的各方,提供如何作出收益最大或損耗最小之決策的一種數學分析方法。它最初討論的是象棋、撲克和橋牌等競爭性娛樂活動的對策。因此,又稱為博奕論。
據《史記》記載:戰國時,齊王與田忌賽馬,雙方都有上、中、下三個等級的馬各一匹,每次雙方出一匹馬參加比賽,共進行三次。雖然田忌的馬都比齊王同一等級的馬差,但是由於田忌的謀士孫臏(著名軍事家)為他設計了如下的對策:用下馬對齊王的上馬;用上馬對齊王的中馬;用中馬對齊王的下馬,田忌反而以2:1取勝。這就是使用對策論思想一個最早的例子。
1943年,馮·諾伊曼與摩根斯頓(O.Morgenstern,美籍德國人,1902—1977)對競爭性經濟活動進行了系統的研究,對策論開始成為一門學科。由於電子計算機的出現,它得到了迅速的發展。
在對策論中,研究對立的雙方在競爭性活動中,各自為制勝對方所取最優策略的存在與求法等問題。例如,對於敵我雙方的潛艇與反潛艇飛機,都存在各自應採取怎樣的航線,使得儘可能保存自己,又能儘量消滅對方的對策問題。
對策論所研究的,可以是由兩方參加的,也可以是由多方參加的競爭活動;而且參加者不一定是完全對立的,還允許他們結成某種聯盟;活動的結局,也可能要參加者通過多次決策才能決定。對控制系統來說,競爭的雙方都不是人,其中一方是客觀環境,另一方是控制系統本身。因此,對策論不僅在軍事(戰術)上,而且在人與自然界作鬥爭,以及經濟學、管理科學以及外交談判、貿易談判中,甚至在社會科學、行為科學(例如罪犯偵緝問題)等各個方面,都得到了套用。
對策問題三要素
對策論的三個基本概念。指對策問題中的局中人、策略和對策的得失。
局中人是指在一局對策(競爭或鬥爭)中,有決策權的參加者.局中人可以是個人,也可是集團。局中人一般用記號Ⅰ,Ⅱ,…表示,而用字母Ⅰ表示所有局中人構成的集合。只有兩個局中人的對策,稱為兩人對策.多於兩個局中人的對策,稱為多人對策。策略是局中人在對策中採用的一個可行的自始至終通盤籌劃的行動方案。局中人策略的全體稱為策略集合,它可以是有限集,也可以是無限集。局中人在一局對策結束時的得失稱為對策的得失。一局對策結束時,每個局中人的“得失”是全體局中人所取定的一組策略的函式,稱為支付函式,亦稱贏得函式.稱贏得函式為連續函式的對策為連續對策。從每個局中人的策略集中各取一個策略組成的策略組,稱為對策的一個局勢。對策的得失是局勢的函式。
策略
策略是動態規劃的基本概念之一。指由每一階段的決策u(x)(i=1,2,…,n)組成的決策函式序列,記為:
P(x)={u(x),u(x),…,u(x)}。
由第k階段開始到終點為止的決策函式序列稱為子策略,記為:
P(x)={u(x),u(x),…,u(x)}。
由第k階段開始到終點的過程,稱為原過程的後部子過程或稱為k子過程。
動態規劃
動態規劃是最佳化理論和運籌學的一 個重要分支,它是解決多階段決策過程的一種最佳化 方法。它的理論根據是L.R.Bellman等人提出的 “最最佳化原理”。動態規劃問題沒有標準的數學構 成,只有求解問題的一般性六個步驟:
(1)將問題恰當地劃分若干階段;
(2)正確地確定每一階段有若干個可能狀態;
(3)每一階段上的決策效益是從一種狀態轉移到下一階段某個狀態時對目標函式所作的貢獻;
(4) 寫出狀態轉移方程;
(5)確定各階段各種決策的直接指標: 列出計算各階段最優策略指標的遞推方法;
(6)求解過程從尋求最後階段的每種狀態下的最優決策開始,按與實際過程相反的方向,向最初階段推移。
近年來,動態規劃在工程技術、經濟、工業生產及軍事等部門都有廣泛套用,並獲得顯著成就。
動態規劃問題可根據決策過程是有限階段或是無限階段而分類;還可根據狀態變數劃分為連續狀態變數問題或離散狀態變數問題;以及是否含有隨機性參量劃分為隨機性和確定性兩類等等。
