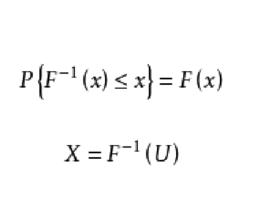基本介紹
反變換法是最常用且最為直觀的一種隨機變數生成方法。它基於 機率積分變換定理,通過對分布函式進行反變換來實現,因此稱為 反變換法。
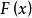 反變換法
反變換法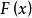 反變換法
反變換法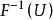 反變換法
反變換法設隨機變數X的分布函式為 ,則 的取值範圍為[0,1]。為了得到隨機變數的抽樣值,可以先產生在[0,1]區間上均勻分布的獨立隨機變數U,根據分布函式的性質,可知其分布函式的反函式 必然滿足
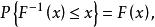 反變換法
反變換法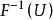 反變換法
反變換法因此,由得到的值即為所需要的隨機變數
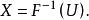 反變換法
反變換法如圖1所示。
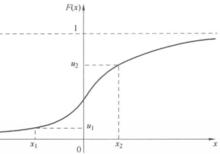 圖1 反變換法的原理
圖1 反變換法的原理生成隨機變數的方法與步驟
反變換法可用於從均勻分布、指數分布、三角分布、威布爾分布以及經驗分布中取樣,同時也是很多離散分布產生樣本的基本方法。下面結合具體的例子來說明生成均勻分布、指數分布和離散均勻分布等幾種隨機變數的方法和步驟。其他幾種分布類型的隨機變數的生成,可自行查閱相關資料。
均勻分布
【 例1】均勻分布隨機變數X的生成。
設隨機變數X是[a,b]上均勻分布的隨機變數,即機率密度函式
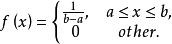 反變換法
反變換法 反變換法
反變換法則由可得到x的分布函式
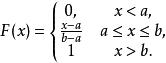 反變換法
反變換法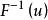 反變換法
反變換法根據其反函式,即有抽樣公式
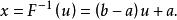 反變換法
反變換法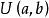 反變換法
反變換法因此,可得採用反變換法生成均勻分布的隨機變數的一般步驟,具體如下:
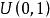 反變換法
反變換法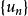 反變換法
反變換法①生成獨立的均勻分布隨機數序列。
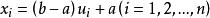 反變換法
反變換法 反變換法
反變換法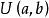 反變換法
反變換法②令。則數列即為所求的均勻分布的隨機變數序列。
指數分布
【 例2】 指數分布隨機變數X的生成。
設X的分布函式為
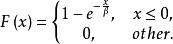 反變換法
反變換法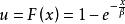 反變換法
反變換法令,可得其反函式
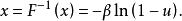 反變換法
反變換法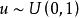 反變換法
反變換法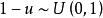 反變換法
反變換法由於,則,即隨機變數u與1-u的分布是相同的,所以上式可改寫為
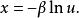 反變換法
反變換法由此,可得到生成指數分布的隨機變數的一般步驟如下:
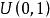 反變換法
反變換法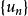 反變換法
反變換法①生成獨立的均勻分布隨機數序列。
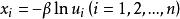 反變換法
反變換法 反變換法
反變換法②令,則數列即為所求的指數分布的隨機變數序列。
離散均勻分布
當X是離散型的隨機變數時,由於離散型隨機變數的分布函式也是離散的,因此反變換法的形式也有所不同,不能直接利用反函式來獲得X的抽樣值。
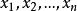 反變換法
反變換法設X是離散型隨機變數,取值為,並記其機率密度函式為
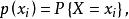 反變換法
反變換法且
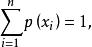 反變換法
反變換法相應的分布函式為
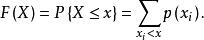 反變換法
反變換法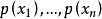 反變換法
反變換法為了套用反變換法得到離散隨機變數X,先將[0,1]區間按的值分成n個子區間
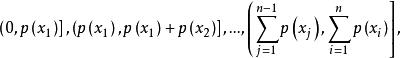 反變換法
反變換法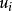 反變換法
反變換法 反變換法
反變換法並依次編號為1,2,…,n。若U是[0,1]區間上的均勻分布隨機變數,則某個的值落在哪個子區間上,相應子區間對應的就是所需要的輸出量。
【 例3】離散均勻分布。
考察{1,2,…,n}上的離散均勻分布,其機率密度函式為
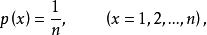 反變換法
反變換法相應的分布函式為
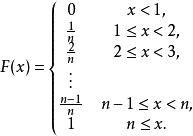 反變換法
反變換法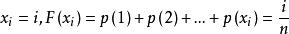 反變換法
反變換法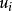 反變換法
反變換法令,如果均勻分布U(0,1)的隨機數滿足
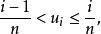 反變換法
反變換法則可以通過取X=i來生成隨機變數X。
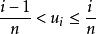 反變換法
反變換法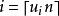 反變換法
反變換法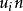 反變換法
反變換法由式可求解得,即取i的值為大於或等於的最小整數。因此,生成離散型均勻分布的隨機變數的一般步驟如下:
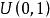 反變換法
反變換法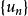 反變換法
反變換法① 生成獨立的均勻分布隨機數序列。
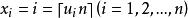 反變換法
反變換法 反變換法
反變換法② 令,則數列即為所求的離散型均勻分布的隨機變數序列。