定義
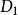 半線性變換
半線性變換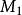 半線性變換
半線性變換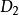 半線性變換
半線性變換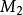 半線性變換
半線性變換 半線性變換
半線性變換 半線性變換
半線性變換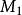 半線性變換
半線性變換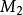 半線性變換
半線性變換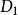 半線性變換
半線性變換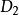 半線性變換
半線性變換 半線性變換
半線性變換稱除環上左向量空間到除環上左向量空間的一個映射為 半線性變換,如果:(1)是加群到加群的同態對應;(2)存在一個到上的同構對應,有
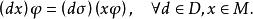 半線性變換
半線性變換 半線性變換
半線性變換 半線性變換
半線性變換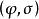 半線性變換
半線性變換如果需要明確指出,則將半線性變換記作。
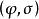 半線性變換
半線性變換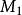 半線性變換
半線性變換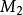 半線性變換
半線性變換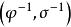 半線性變換
半線性變換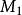 半線性變換
半線性變換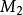 半線性變換
半線性變換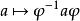 半線性變換
半線性變換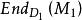 半線性變換
半線性變換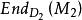 半線性變換
半線性變換若是到上的一對一的、半線性變換,則易見是到上的一對一的、半線性變換而對應是環到上的同構對應 。
相關定理
命題1
 半線性變換
半線性變換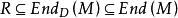 半線性變換
半線性變換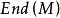 半線性變換
半線性變換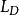 半線性變換
半線性變換設是除環D上左向量空間,若且R是二重傳遞環,則R在內的中心化子恰是。
定理1
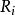 半線性變換
半線性變換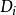 半線性變換
半線性變換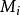 半線性變換
半線性變換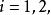 半線性變換
半線性變換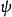 半線性變換
半線性變換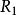 半線性變換
半線性變換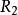 半線性變換
半線性變換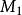 半線性變換
半線性變換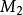 半線性變換
半線性變換 半線性變換
半線性變換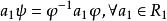 半線性變換
半線性變換(唯一性定理) 是除環上左向量空間的稠密環;且有極小單側理想,若是環到上的一個同構對應,則必存在到上的一個一對一的、半線性變換,使。
定理2
 半線性變換
半線性變換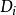 半線性變換
半線性變換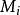 半線性變換
半線性變換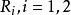 半線性變換
半線性變換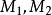 半線性變換
半線性變換 半線性變換
半線性變換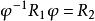 半線性變換
半線性變換若把有極小單側理想的本原環表成除環上左向量空間上的稠密環,則在向量空間間必存在一個一對一的、半線性變換且。
命題2
設R是除環D上左向量空間M的二重傳遞線性變換環,則R是D上空間M的稠密環。
定理3
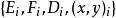 半線性變換
半線性變換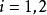 半線性變換
半線性變換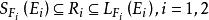 半線性變換
半線性變換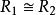 半線性變換
半線性變換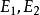 半線性變換
半線性變換 半線性變換
半線性變換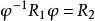 半線性變換
半線性變換設是對偶空間,,而且,則空間之間必存在一個一對一的、半線性變換且有。

