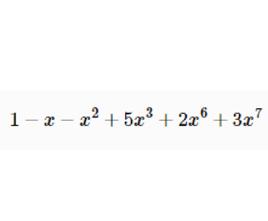定義
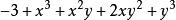 升冪
升冪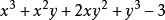 升冪
升冪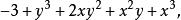 升冪
升冪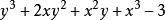 升冪
升冪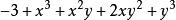 升冪
升冪把一個多項式按某一個字母的指數從大到小的順序排列起來,叫做把這個多項式按這個字母降冪排列,簡稱“ 降冪”;把一個多項式按某一個字母的指數從小到大的順序排列起來,叫做把多項式按這個字母升冪排列,簡稱“ 升冪”。如 ,按x的降冪排列是 ,按x的升冪排列是 按y的降冪排列是 ,按y的升冪排列是 。
理論根據
把一個多項式按某一個字母升(降)冪排列的理論根據是加法的交換律和結合律。
詳細介紹
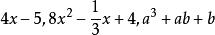 升冪
升冪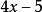 升冪
升冪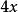 升冪
升冪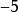 升冪
升冪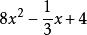 升冪
升冪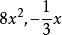 升冪
升冪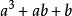 升冪
升冪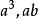 升冪
升冪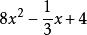 升冪
升冪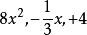 升冪
升冪在整式 中,都含有加減運算,它們都不是單項式,而可以看作是幾個單項式的和。例如 是單項式 與 的和, 是單項 與+4的和; 是單項式 與+b的和,幾個單項式的和叫做 多項式,其中每個單項式都叫做 多項式的項。例如對於多項式來說, 就都是它的項。
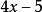 升冪
升冪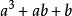 升冪
升冪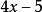 升冪
升冪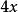 升冪
升冪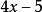 升冪
升冪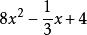 升冪
升冪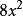 升冪
升冪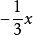 升冪
升冪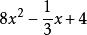 升冪
升冪一個多項式含有幾項,就叫做 幾項式。例如 含有兩項,叫做 二項式, 含有三項,叫做 三項式。在二項式 中,第一項 的次數是1,叫做 一次項,第二項-5沒有字母,叫做 零次項或 常數項。這裡次數最高的是一次項,所以叫做 一次二項式。在三項式中,第一項的次數是2,叫做二次項,是一次項,+4是常數項.這裡次數最高的是二次項,所以叫做 二次三項式。總之,一個多項式里次數最高的項的次數,叫做這個 多項式的次 數,多項式的次數是幾,就叫做 幾次多項式。
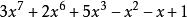 升冪
升冪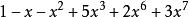 升冪
升冪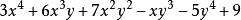 升冪
升冪為了運算的方便,通常把一個多項式的項按照某種順序排列起來,對於只含一個字母的多項式,可以按照各項次數的高低,由高到低或由低到高地排列。前一種叫做 降冪排列,後一種叫做 升冪排列。例如,就是降冪排列,而就是升冪排列。對於含有幾個字母的多項式,若各項所含的字母不全相同,那么可以先就其中某一個字母降冪或升冪排列,餘下的項再依次就第二、第三、……個字母降冪或升冪排列。例如,就是就x降冪排列所得。
意義
把一個多項式按某一個字母升(降)冪排列的意義:
一是能使計算方便;
二是採用這種約定俗成的排列習慣能避免雜亂,能使多項式的排列有條理,富有美感。
例題解析
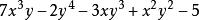 升冪
升冪例1 把多項式 。
(1)按y的降冪排列;(2)按x的升冪排列。
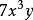 升冪
升冪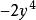 升冪
升冪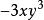 升冪
升冪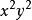 升冪
升冪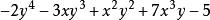 升冪
升冪分析:(1) 是y的一次項, 是y的四次項, 是y的三次項, 是y的二次項,-5是常數項,是y的0次項,按y的降冪排列是 ;
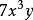 升冪
升冪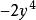 升冪
升冪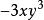 升冪
升冪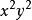 升冪
升冪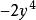 升冪
升冪(2) 是x的三次項, 中沒有x,當成x的0次項, 是x的一次項, 是x的二次項,-5是常數項,是x的0次項,這裡 與-5都不含z,但在升冪排列中,按習慣應將-5寫在最前面。
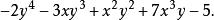 升冪
升冪解: (1)
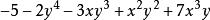 升冪
升冪(2) .
這類題目必須先弄清兩點:(1)關注的是哪個字母;(2)是升冪還是降冪。
 升冪
升冪例2 將 降冪排列。
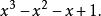 升冪
升冪錯解:
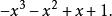 升冪
升冪正解:
分析:降冪排列時,是按降冪要求交換加數的位置,交換時要連同它們的符號一起交換。