匈牙利解法的適用條件
匈牙利解法的適用於基於任務分配問題的標準型，標準型要滿足下述三個條件：
（1）目標要求為min；
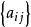匈牙利解（2）效率矩陣 為n階方陣；
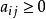匈牙利解（3）陣中所有元素 ，且為常數。
求解步驟
指派問題的匈牙利法求解步驟：
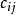匈牙利解
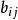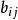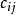匈牙利解 匈牙利解 匈牙利解（1）變換指派問題的係數矩陣( ) 為( ) ，使在( ) 的各行各列中都出現0元素，即從( )的每行元素都減去該行的最小元素；再從所得新係數矩陣的每列元素中減去該列的最小元素。
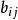匈牙利解
匈牙利解（1）進行試指派，以尋求最優解。在( )中找儘可能多的獨立0元素，若能找出n 個獨立0元素，就以這n 個獨立0元素對應解矩陣( )中的元素為1，其餘為0，這就得到最優解。
找獨立0元素，常用的步驟為：
1) 從只有一個0元素的行開始，給該行中的0元素加圈，記作◎ 。然後划去◎ 所在列的其它0元素，記作Ø ；這表示該列所代表的任務已指派完，不必再考慮別人了。依次進行到最後一行。
2) 從只有一個0元素的列開始（畫Ø的不計在內），給該列中的0元素加圈，記作◎；然後划去◎ 所在行的0元素，記作Ø ，表示此人已有任務，不再為其指派其他任務了。依次進行到最後一列。
3) 若仍有沒有劃圈的0元素，且同行(列) 的0元素至少有兩個，比較這行各0元素所在列中0元素的數目，選擇0元素少這個0元素加圈(表示選擇性多的要“禮讓”選擇性少的) 。然後劃掉同行同列的其它0元素。可反覆進行，直到所有0元素都已圈出和劃掉為止。
4) 若◎ 元素的數目m 等於矩陣的階數n （即：m =n ），那么這指派問題的最優解已得到。若m < n，則轉入下一步。
（3）用最少的直線通過所有0元素。其方法：
1) 對沒有◎的行打“√”；
2) 對已打“√” 的行中所有含Ø元素的列打“√” ；
3) 再對打有“√”的列中含◎ 元素的行打“√” ；
4) 重複1)、2)直到得不出新的打√號的行、列為止；
5) 對沒有打√號的行畫橫線，有打√號的列畫縱線，這就得到覆蓋所有0元素的最少直線數 l。
註：l 應等於m ，若不相等，說明試指派過程有誤，回到第2步，另行試指派；若l =m < n ，表示還不能確定最優指派方案，須再變換當前的係數矩陣，以找到n 個獨立的0元素，為此轉第（4）步。
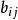匈牙利解（4）變換矩陣() 以增加0元素。在沒有被直線通過的所有元素中找出最小值，沒有被直線通過的所有元素減去這個最小元素；直線交點處的元素加上這個最小值。新係數矩陣的最優解和原問題仍相同。轉回第（2）步 。
示例
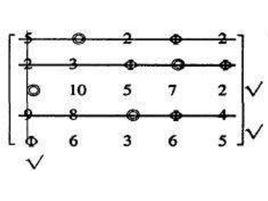
求解下圖問題。
匈牙利解（1）將這係數矩陣進行變換，使各行各列都出現0元素．從係數矩陣的每行元素減去該行的最小元素即得每行每列都有有0元素的係數矩陣。
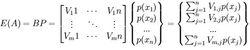匈牙利解（2）進行試指派，找出獨立的0元素。獨立0元素用Θ表示，其它0用Φ表示得到（矩陣(1)）。
匈牙利解這裡Θ的個數m=4，而n=5；問題沒有得到求解，運用步驟（3）繼續求解。
（3）作最少的直線覆蓋所有的0元素，以確定該係數矩陣中能找到最多的獨立元素數．為此按以下步驟進行．
(1) 對沒有Θ的行打√號：；
(2) 對已打√號的行中所含0元素的列打√號；
(3) 再對所有打√號的列中的含有@元素的行打√號；
(4) 重複2、3直到得不出新的打√號的行列為止．
(5) 對沒有打√號的行畫一橫線，有打√號的列畫一縱線，這就得到覆蓋所有0元素的最少直線數．
令直線數為 l。若 l< n，說明必須再變換當前的係數矩陣，才能找到n個獨立的0元素，為此轉換步驟四；若 l= n，而 m< n，應回到步驟（2），另行試探。
在此例中，對矩陣(1)按以下次序進行：先在第五行旁打√，接著可判斷應在第一列下打√，接著在第3行旁打√，經檢查不能再打√了．對沒有打√行畫一直線以覆蓋0元素，對打√的列畫一直線以覆蓋0元素，得（矩陣(2)）：
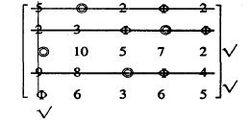匈牙利解由此可見 l= 4 < n．所以應繼續對矩陣(2)進行變換轉步驟（4）。
（4）對矩陣(2)進行變換的目的是增加0元素。
為此在沒有被直線覆蓋的部分中找出最小元素，然後在打√行各元素中都減去這個最小元素，而在打√列的各元素上都加上這個最小元素，以保證原來0元素不變。這樣得到新係數矩陣(它的最優解和原問題相同)．若得到n個獨立的0元素，則已得最優解，否則回到步驟三重複進行。
在矩陣(2)中，在沒有被覆蓋部分(第3、5行)中找到最小元素為2，然後在第3、5行各元素分別減去2。給第l列各元素加2，得到新矩陣(3)：
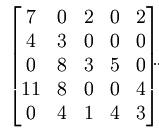匈牙利解按步驟（2），找出所有的獨立0元素。得到矩陣(4)：
匈牙利解它具有n個獨立0元素．這就得到了最優解，相應解矩陣為：
匈牙利解由解矩陣得最優指派方案： 甲——B，乙——D，丙——E，丁——C，戊——A，所需總時間為minz=32。
