包絡
包絡是由許多橢圓形曲線交織而成的一種圖形,外觀看起來是包起來的一樣。包絡在數學、信號處理、文學、經濟學、傳統中醫學上都有自己獨特的含義。
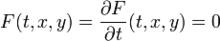 包絡線所滿足的方程
包絡線所滿足的方程在數學上,一族平面直線(或曲線)的“包絡”(envelope)是指一條與這族直線(或曲線)中任意一條都相切的曲線。假設這族平面曲線記為 F( t, x, y),這裡不同的 t對應著曲線族中不同的曲線,則包絡線上的每一點滿足右下端的兩條方程,由這兩條方程消去 t後便可得出包絡線的隱式表示。
類似地可以定義空間中一族平面(或曲面)的包絡。
如圖1中的直線組成一個圈,然而實際上我們並沒有“畫”這個圓,這時就把這個圓稱作是包絡線。
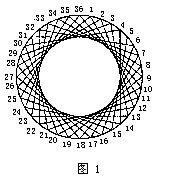 數學中包絡線的示意圖
數學中包絡線的示意圖要想畫出類似的包絡線,首先要畫出一個大圓(例如直徑10cm),並把圓周分成36等分,用量角器每10°作一點即可。
把第n點與第n+10點連線,就可畫出如圖1的圓形包絡線。如果n+10大於36,則須減去36。例如當n=29時,n+10=39,減去36之後得到3,所以第29點是與第3點連線。
包絡面
在波的傳播過程中,總可以找到同相位各點的幾何位置,這些點的軌跡是一個等相位面,叫做波面(即包絡面)。由科學家惠更斯提出。
原始的惠更斯原理是比較粗糙的,用它只能解釋波繞過障礙物的非直線傳播,而不能解釋衍射現象產生的明暗條紋。
由於惠更斯原理的次波假設不涉及波的時空周期特性——波長,振幅和位相,雖然能說明波在障礙物後面拐彎偏離直線傳播的現象,但實際上,光的衍射現象要細微的多,例如還有明暗相間的條紋出現,表明各點的振幅大小不等,對此惠更斯原理就無能為力了。因此必須能夠定量計算光所到達的空間範圍內任何一點的振幅,才能更精確地解釋衍射現象。
包絡環
 包絡環
包絡環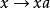 包絡環
包絡環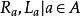 包絡環
包絡環包絡環(enveloping ring)研究無限維代數的一個工具。若A是結合環,則A的變換Ra :與La: 是加群(A,+)的自同態。由集合{}在(A,+)的自同態環End (A , +)中所生成的子環:
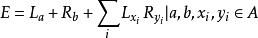 包絡環
包絡環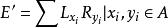 包絡環
包絡環稱為A的包絡環。稱為A的簡包絡環,它是包絡環的子環。當A有單位元時,E=E'。域F上中心單代數A的簡包絡環E'是F上向量空間A的稠密環。.
