簡單介紹
電子透過勢壘的機率就可以用貫穿係數 T來說明。
電子貫穿係數 T隨勢壘寬度 a的增加而迅速減小,下表給出的是( U0- E)=5eV時的具體數據。
| a (nm) | T |
| 0.1 | 0.1 |
| 0.5 | 1.7×10-38 |
| 1.0 | 3.0×10-38 |
勢壘很寬或能量差很大或粒子質量很大時,貫穿係數 T≈0,隧道效應在實際上已經沒有意義,量子概念過渡到經典力學情形。因此,粒子的隧道效應是微觀粒子的量子力學行為,巨觀粒子是不會發生隧道貫穿效應的 。
根本原因
勢壘貫穿的根本原因是“測不準原理”,只要你認可測不準原理,就很容易理解勢壘貫穿了,並不需要你去了解複雜的薛丁格方程求解。解釋如下:能量E與時間T是不能同時測準的,時間測量越準確(時間範圍越短),相應的能量就會無法很準確測量。這裡的測不準並不是技術上的問題,而是“測不準原理”產生的真實的範圍變化。也就是說,微觀粒子在極短的時間內,其能量的可能值範圍就會變大,因此,雖然微觀粒子的能量E小於勢壘U,這裡的粒子能量E應該是其可能的能量範圍的平均值。在極短的時間內,粒子會有一個較小的幾率處於這個能量範圍的高端處(即呈現高能狀態),瞬間能量超過了勢壘U。如果勢壘U的空間跨度非常小,這個只能存在極短時間的高能粒子將可以越過勢壘,越過勢壘之後,粒子的能量重新回復到正常大小。簡單地說,就是先憑空”借”來能量,成功穿越後再把“借”來的能量”還”回去,這種憑空的能量“借還”是可以允許的,也並沒有違背能量守恆原理,但必須在極短的時間之內進行,因此勢壘貫穿現象能夠穿越的距離也就非常小。
這種憑空的能量借還的現象也是量子理論中“虛粒子”的產生原因——在極短時間內,真空中某處會突然處於高能狀態,這些能量轉換成一對正粒子和反粒子,然後這對粒子又立刻相互湮滅而消失,這就是“虛粒子”。這就是量子理論對於”真空”的描述,真空中無時不刻地大量出現這種虛粒子。虛粒子對巨觀真空不會產生任何影響,但對於微觀下的量子真空卻有極深遠的意義。
勢壘貫穿問題分析
 勢壘貫穿
勢壘貫穿 勢壘貫穿
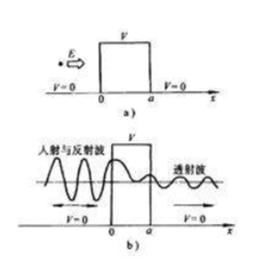
勢壘貫穿設具有一定能量E的粒子沿x軸正向射向勢壘,按經典力學若 ,則粒子將不能進入勢壘,將被彈回去;若 ,則粒子將穿過勢壘。
 勢壘貫穿
勢壘貫穿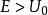 勢壘貫穿
勢壘貫穿但從量子力學觀點,考慮到粒子的波動性,此問題像波碰到一層厚度為a的介質相似,有一部分波透過,一部分波被反射回去。所以,按量子力學的觀點,因波函式的統計解釋,無論粒子能量 或 ,都有一定的幾率穿透勢壘,也有一定的幾率被反射,這就是勢壘貫穿問題,也叫一維散射問題。
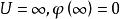 勢壘貫穿
勢壘貫穿本問題與無限保勢阱及一維諧振子的問題不同,在前兩個問題中,在無窮大處 。這使得體系的能級是分立的。但現在的情況是,體系在無窮大處勢能有限(這裡取為0),此時,粒子可以出現在無限遠處,由此使得體系的能量可以取任意值,即組成連續譜,可以預先確定粒子的能量值。
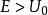 勢壘貫穿
勢壘貫穿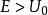 勢壘貫穿
勢壘貫穿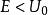 勢壘貫穿
勢壘貫穿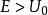 勢壘貫穿
勢壘貫穿1. 對本問題的討論,按 和 分開討論,是討論 情況,可按三個步驟進行。
(1)寫出體系的定態薛丁格方程,並作適當變換;
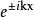 勢壘貫穿
勢壘貫穿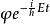 勢壘貫穿
勢壘貫穿(2)進行求解:在求解過程中,注意這裡方程的形式與無限保勢阱時方程的形式一致。但這裡的解用了 的形式,而未用coskx或sinkx的形式。這因為現在的情況是,在無窮大處,粒子應為自由粒子,其波函式應為動量本徵態,即其解為平面波的形式;而無限保勢阱中,是束縛態,其能級作簡併,解的形式應為coskx或sinkx 。由此,寫出了三個不同區域的解的形式,而定態函式即為 。
(3)確定上述三個解中的待定係數,這可由物理實際和邊界條件確定。
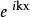 勢壘貫穿
勢壘貫穿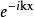 勢壘貫穿
勢壘貫穿首先是由解的物理意義確定c:上述三個解的第一項是 的形式,是代表向右(沿x正方向)傳播的平面波,x第二項是 的形式,代表向左傳播的平面波。
 勢壘貫穿
勢壘貫穿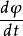 勢壘貫穿
勢壘貫穿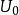 勢壘貫穿
勢壘貫穿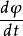 勢壘貫穿
勢壘貫穿在x>a區域內,實際上沒有向左運動的粒子,應令c=0,其次,由邊界條件確定常數。邊界條件是:在x=0和x=a處, 及 (在勢場 在跳躍 的不連續點,仍應保持連續)應連續,由此列出了四個方程,但有五個未知數。但這沒有關係,量子力學中關心的是粒子出現在不同位置的幾率(相對幾率)這裡特別關心給定入射波後,反射波和透射波的情況。即只要關心x<0區域中的反射波和x>a區域中的透射波與入射波的關係,為此,由上述四個方程可確定如下關係:
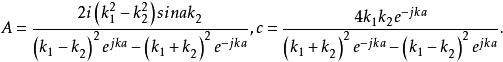 勢壘貫穿
勢壘貫穿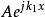 勢壘貫穿
勢壘貫穿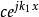 勢壘貫穿
勢壘貫穿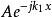 勢壘貫穿
勢壘貫穿 勢壘貫穿
勢壘貫穿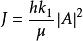 勢壘貫穿
勢壘貫穿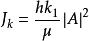 勢壘貫穿
勢壘貫穿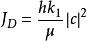 勢壘貫穿
勢壘貫穿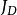 勢壘貫穿
勢壘貫穿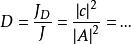 勢壘貫穿
勢壘貫穿由此給出了反射波和透射波與入射波的振幅關係,將入射波 ,透射波 和反射波 依次代入J公式中的 ,分別得到入射波的幾率密度為 僅反射波的幾率流密度為 透射波的幾率流密度為: ,於是 與J之比,即透射係數為 同理可得反射係數R可以驗證R+D=1。
D表示粒子透過勢壘的幾率,R表示粒子波反射回去的幾率,上式正是幾率守恆的表現。
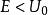 勢壘貫穿
勢壘貫穿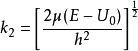 勢壘貫穿
勢壘貫穿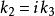 勢壘貫穿
勢壘貫穿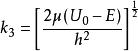 勢壘貫穿
勢壘貫穿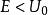 勢壘貫穿
勢壘貫穿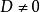 勢壘貫穿
勢壘貫穿2. 的情況此時,前述 為虛數,只要令 為實數,同理可得R,D0可見,即使 ,在一般情況下,也有 。粒子能穿透比其動能更高的勢壘的現象,叫隧道效應,它是粒子具有波動性的表現,這在經典物理中是無法解釋的。
由此可見:勢壘加寬,即a升高或勢壘加高,均有D下降,如果勢壘不是方勢壘,則可以算作是許多方勢壘(寬為dx,高為U(x))組成的。