詳解
此穩定性判據之所以重要，是因為若線性系統之特徵方程式的根 p均有負的實部，表示其解 e為穩定的（BIBO穩定）。 因此穩定性判據提供了方式，可以在不求解線性系統的運動方程的情形下，判斷其是否只有穩定解。對於離散系統，對應穩定性的測試可以由Schur–Cohn判據、Jury穩定性判據及Bistritz穩定性判據來判斷。隨著電腦的進步，此穩定性判據變的較少使用，另一種判斷的方式則是用數值方法直接求解多項式，得到其解的近似值。
勞斯測試可以由輾轉相除法以及在計算柯西指標時用施圖姆定理來推導。赫爾維茨利用另一種方式來推導其穩定性判據。
利用輾轉相除法求解
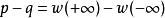勞斯–赫爾維茨穩定性判據勞斯–赫爾維茨穩定性判據和勞斯–赫爾維茨定理有關。由定理的陳述，可得 其中：
1）p為多項式 ƒ( z)的根中實部為負值的個數。
2）q為多項式 ƒ( z)的根中實部為正值的個數。（此假設 ƒ( z)的根都不在虛軸上）
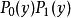勞斯–赫爾維茨穩定性判據
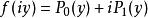勞斯–赫爾維茨穩定性判據3）w(x)為 由施圖姆定理得到的變號數（中間利用連續的輾轉相除法），其中 ， y為實數。
根據代數基本定理，每個 n次的多項式在複數平面上會有 n個根（也就是，對於根都不在虛軸上的 ƒ， p+ q= n）。因此可得到 ƒ為（穩定的）赫爾維茨多項式若且唯若 p− q= n。利用勞斯–赫爾維茨定理，可以將 p和 q的條件改為以廣義施圖姆鏈組成的條件，也就是以 ƒ的係數組合而成的條件。
使用矩陣
令 f( z) 為一個復多項式。過程如下：
1）計算多項式和使得
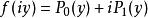勞斯–赫爾維茨穩定性判據其中 y為一實數。
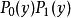勞斯–赫爾維茨穩定性判據2）計算與相關的西爾維斯特矩陣。
3）重新排列每一行，讓奇數行和其下一行起始地零數量相同。
4）計算該矩陣的每個主子式。
5）如果這些子式中至少一個為負（或零），則多項式 f是不穩定的。
範例
1）令(為了簡單起見，我們取實係數），其中
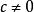勞斯–赫爾維茨穩定性判據 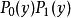勞斯–赫爾維茨穩定性判據（為了避免一根為零，我們可以利用勞斯–赫爾維茨定理）。首先，我們要計算實多項式 ：
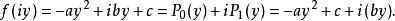勞斯–赫爾維茨穩定性判據2）接下來，我們將多項式輾轉相除來得到廣義施圖姆鏈：
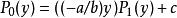勞斯–赫爾維茨穩定性判據
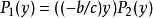勞斯–赫爾維茨穩定性判據
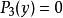勞斯–赫爾維茨穩定性判據得到 ，於是輾轉相除法結束。
注意我們在第一次除法中，必須假設 b不為零。在此情形下，廣義施圖姆鏈為
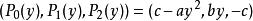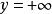勞斯–赫爾維茨穩定性判據
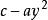勞斯–赫爾維茨穩定性判據
勞斯–赫爾維茨穩定性判據
勞斯–赫爾維茨穩定性判據令， 的符號與 a相反，而 by的符號與 b相同。當我們令時，該鏈的第一部分符號也與 a相反，而 by的符號與 b相反。最終，- c的符號總與 c相反。
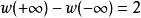勞斯–赫爾維茨穩定性判據
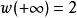勞斯–赫爾維茨穩定性判據
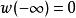勞斯–赫爾維茨穩定性判據現在假設 f是赫爾維茨穩定的。這意味著（f的階數）。由函式w的性質，這與及相同。因此， a, b和 c必須符號相同。我們找到了二階多項式穩定的必要條件。
高階多項式的勞斯–赫爾維茨判據
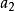勞斯–赫爾維茨穩定性判據
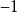勞斯–赫爾維茨穩定性判據在下面，我們假設最高階的係數（例如二階多項式中的 ）為正。如果有必要，總可以將該多項式乘以 得到。
1）對於二階多項式
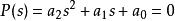勞斯–赫爾維茨穩定性判據如果所有係數都滿足：
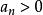勞斯–赫爾維茨穩定性判據
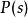勞斯–赫爾維茨穩定性判據則所有根都在左半平面（特徵方程為 的系統穩定）.
2）對於三階多項式
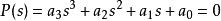勞斯–赫爾維茨穩定性判據所有係數都滿足
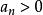勞斯–赫爾維茨穩定性判據並且有
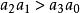勞斯–赫爾維茨穩定性判據3）對於四階多項式
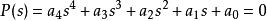勞斯–赫爾維茨穩定性判據所有係數都滿足
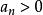勞斯–赫爾維茨穩定性判據並且
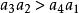勞斯–赫爾維茨穩定性判據且
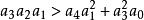勞斯–赫爾維茨穩定性判據4）一般地，勞斯穩定性判據要求勞斯表的第一列所有元素符號相同。
滿足上述判據的系統稱為閉環穩定系統，否則會由於第一列元素符號改變而不穩定。
