赫爾維茨公式(是把兩個緊黎曼面(即光滑射影曲線)的虧格與它們的覆蓋次數和分歧點重數相聯繫的公式.設R}R是兩個緊黎曼面的m重有分歧的覆蓋,分歧點的重數為kl}kz,...,k.},則有公式
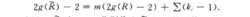 赫爾維茨公式
赫爾維茨公式這裡g(R)和g(R)分別代表反和R的虧格.
赫爾維茨公式穩定性判定:
設系統的特徵方程式為
 赫爾維茨公式
赫爾維茨公式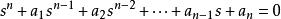 赫爾維茨公式
赫爾維茨公式以特徵方程的各項係數組成如下行列式:
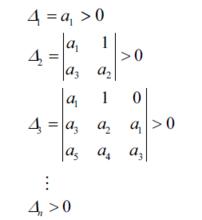 各階子式行列式
各階子式行列式其各階子行列式滿足下列條件:
赫爾維茨穩定判據指出,系統穩定的充分必要條件是在上述行列式的各階主子式△i均大於零 。
證明赫爾維茨穩定性判據的方法是用李雅普諾夫第二法,
(1)將給定的描述系統運動的高階齊次微分方程變換為齊次狀態方程。
(2)給定對稱正定(或非負定)矩陣Q,根據式(1)求出相應的矩陣P。
(3)由要求矩陣P 為正定的條件證明赫爾維茨穩定判據 。
 赫爾維茨公式
赫爾維茨公式赫爾維茨公式的演變:赫爾維茨 函式
 赫爾維茨公式
赫爾維茨公式 赫爾維茨公式
赫爾維茨公式 赫爾維茨公式
赫爾維茨公式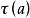 赫爾維茨公式
赫爾維茨公式著名學者S.Kanemitsu 教授和M.Yoshimoto 博士曾研究得出了一些關於赫爾維茨 函式部分的定理和結論,關於這些結論套用於雙 函式導數的計算、廣義黎曼 函式導數性質的研究以及套用於函式理論的充實與完善都很有意義。
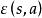 赫爾維茨公式
赫爾維茨公式 赫爾維茨公式
赫爾維茨公式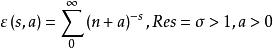 赫爾維茨公式
赫爾維茨公式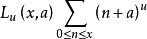 赫爾維茨公式
赫爾維茨公式 赫爾維茨公式
赫爾維茨公式記為赫爾維茨函式,定義,並且在除s=1的簡單極點外的複平面上亞頓連續,而記為赫爾維茨函式的部分和,其中u代表復變數,a>0,x≥0。 。
