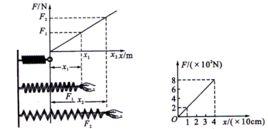
相關公式
參見胡克定律
其中，F為彈力，k是勁度係數，△x是彈簧形變數
套用學科：高中物理；水利科技（一級學科）；工程力學、工程結構、建築材料（二級學科）；工程力學（水利）（三級學科）
串聯與並聯
兩彈簧勁度係數分別為k，k
兩彈簧串聯後
k=（k×k）/（k+k）
兩彈簧並聯後mg=F1+F2=(K1+K2)X
k=k+k
單位
牛頓/米（N/m）
影響因素
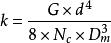勁度係數（N/mm）
其中：
G=線材的剛性模數，單位N/mm^2（即切變模量）：碳素彈簧鋼絲（如65Mn）以及常用彈簧鋼絲79000 ；不鏽鋼絲71000 ，矽青銅線G=41000 【其他詳見機械設計手冊（第五版）第三卷P11-10】
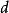勁度係數=線徑（mm）
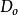勁度係數=外徑（mm）
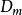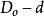勁度係數
勁度係數=中徑=（mm）
N=總圈數
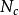勁度係數=有效圈數=N-2
彈簧常數計算範例: 線徑=2.0mm , 外徑=22mm , 總圈數=5.5圈 ,鋼絲材質=琴鋼絲
在彈性限度內，彈簧的彈力可由F=kX,x為彈簧的伸長的長度；k為勁度係數，表示彈簧的一種屬性，它的數值與彈簧的材料，彈簧絲的粗細，彈簧圈的直徑，單位長度的匝數及彈簧的原長有關。在其他條件一定時彈簧越長，單位長度的匝數越多，k值越小。
k還與 溫度 有關，其他條件一定時，溫度越低k越大．
相關例題
1、 將一個勁度係數為K的彈簧一截為二，則一半長的彈簧的勁度係數為多少，是原勁度係數的兩倍嗎？
2． 將兩根勁度係數分別為K1和K2的彈簧兩端固定，在兩彈簧中間連線一個質量為m的物體，合成後的彈簧的勁度係數為多少，等於K1和K2的和嗎？
3． 將兩根勁度係數分別為K1和K2的彈簧直接相連，一端固定，一端連線質量為m的物體，合成後的彈簧的勁度係數為多少，等於K1*K2/（K1+K2）嗎？
4． 把一根彈簧在其一半處摺疊成一根雙股彈簧，則其彈簧的勁度係數為多少，等於原來的兩倍嗎？
解答
第1題：原彈簧可以看作兩個“半彈簧”串接，設勁度係數為k1=k2,當原彈簧受力變形時，每個“半彈簧”變形量為x，則整個彈簧變形為2x。則有
F=K*(2x)=k1*x=k2*x，k1=k2=2K
每個彈簧勁度係數都是2K。注意這樣串聯的兩個“半彈簧”受力大小是一致的。推廣而言我們可以求更一般的情況——彈簧不是對半開，而是一定的比例，變形量比例與原長比例一致。
第2題：兩個彈簧變形量x一致，只不過一個為拉伸則另一個為壓縮，但產生的力是方向一致，按照力等效的觀點，則K1*x+K2*x=K*x，所以K=K1+K2。
第3題：原理同第1題，正屬於我所說的推廣情況。K*(x1+x2)=K1*x1=K2*x2=F，故F/K=(F/K1+F/K2)，即K=K1*K2/(K1+K2)。
第4題：變形一致，總的力=兩個分力之和。故K*x=K1*x+K2*x，K=K1+k2；由第1題可知K1=K2是原彈簧的2倍，到此題K就是原彈簧的4倍。
