線性系統
設系統的微分方程如下：
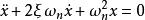相軌跡
相軌跡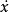
相軌跡取相坐標 、 ，上述方程可化為
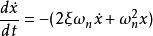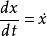相軌跡
相軌跡或
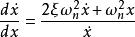相軌跡根據系統的不同特性，相軌跡主要有以下三種情況：1. 無阻尼 2. 欠阻尼 3. 過阻尼
無阻尼運動
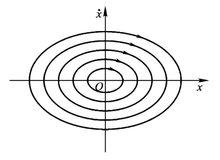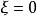相軌跡
相軌跡無阻尼系統的 ，因此方程變為：
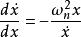相軌跡通過求解微分方程可以得到系統相軌跡方程為：
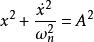相軌跡
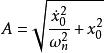相軌跡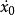
相軌跡
相軌跡式中 為由初始條件 、 決定的常數。
特性：
1. 相軌跡垂直穿過橫軸
2. 在坐標原點處有唯一孤立奇點
欠阻尼運動
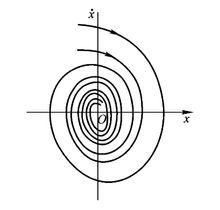相軌跡對方程進行求解得到相軌跡：
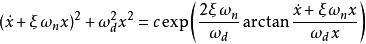相軌跡式中
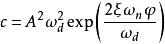相軌跡特性：
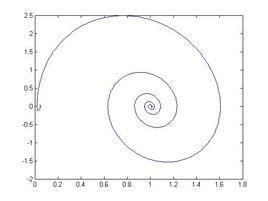
不管系統的初狀態如何，經過一些衰減震盪，最後趨向於平衡狀態。坐標原點是一個奇點，它附近的相軌跡是最終收斂於它的對數螺旋線（將相軌跡化為極坐標可看出），這種奇點稱為穩定的焦點 。
過阻尼運動
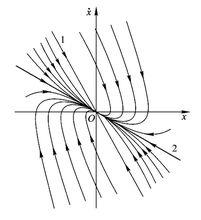相軌跡通過求解微分方程可以得到相軌跡方程為：
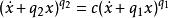相軌跡式中
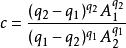相軌跡特性：
相軌跡為一簇拋物線，系統從任一初始狀態出發，非周期的趨向於平衡狀態。坐標原點為奇點，這種奇點稱為穩定的節點 。
非線性系統
繼電型系統
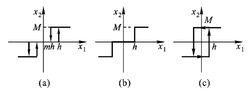相軌跡繼電型系統的非線性特性如上圖所示。圖(a)對應的數學表達式為
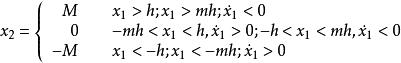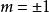相軌跡
相軌跡當 時可分別得到圖(b)和圖(c)
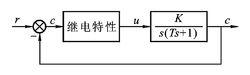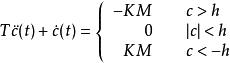相軌跡
相軌跡若系統的方框圖如上所示，則圖(b)系統的微分方程為 ，相軌跡如下圖所示
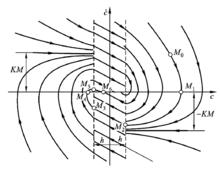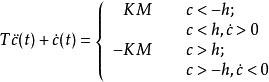相軌跡
相軌跡圖(c)系統的微分方程為 ，相軌跡如下圖所示
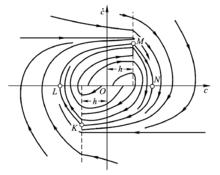相軌跡作圖方法
相軌跡的作圖方法可分為：解析法和圖解法，其中解析法主要針對可直接由方程求出 關係的、相對比較簡單的系統，而圖解法則針對不能直接由方程求出 關係的系統，原則上說，此法對任何非線性系統都適用，圖解法根據具體的作圖方法不同，可進一步分為等傾斜線法 , δ 法。下面介紹這三種方法。
解析法
適用於簡單的二階線性系統或是分段線性系統（如繼電型系統），可以通過微分方程求的相軌跡的表達式。但是一般來說求出微分方程的解析解是比較困難的，所以解析法具有較大的局限性，因此對於非線性系統常採用等傾斜線法來畫相軌跡圖像或者採用描述函式法進行近似分析。
等傾斜線法
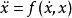相軌跡等傾斜線法適用於下述一般形式的系統 ：
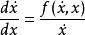相軌跡其基本思想是：考慮相軌跡通過相平面上的點，令 是常數，即相軌跡通過該點的斜率一定。分別取不同的斜率繪製曲線，這些線稱為等傾斜線。在每條等傾線上畫出表示斜率值的小線段，並進行光滑連線，就得到所求的相軌跡和相平面圖。
其它
特徵根和奇點對應關係
二階系統的特徵根位置和奇點類型對應關係如下圖所示
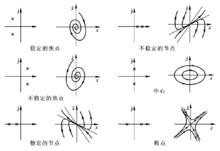相軌跡