簡介
分次環與模最初發展的主要動力是交換代數幾何中的射影代數簇,並形成代數幾何研究中的基本方法之一自20世紀70年代以來,(群)分次環和模的發展進人了一個嶄新的時期,主要來自非交換代數幾何及群表示理論的推動.群分次環理論非常活躍且富有成果,在這一發展階段中代表人物有奧西塔因(F. Van.Oystaeyen)、納斯塔西庫(C.Nastasescu )、達第(E. C.Dade 、蒙哥馬利(S.Montgomery )、科恩(Cohen, M.)和帕斯曼(D. S.Passman)等.群分次環以其與眾多數學分支的密切聯繫而引起人們的極大興趣.
實例
例如:
1.相伴於濾子化環的Z分次環理論是李代數、代數幾何尤其是層理論、微分方程尤其是微分運算元環等理論研究中的有力工具。
2.非交換環的任意群分次的理論在群作用於環及不動點(環)、群表示理論尤其是穩定克利福德理論等發揮了重要的作用。
3.非交換環的有序群分次的理論及由此而產生的分次序理論是數論、代數表示論、非交換代數幾何、維數理論和環理論的一個重要的基本成分。
4一般群分次理論與霍普夫代數、馮·諾伊曼代數等理論有著深刻的聯繫。
值得一提的是,分次環的理論固然重要,而更重要的是分次環的研究方法,這一點可以從分次環的廣泛而富有意義的套用中看出 。
第一個屬性
讓
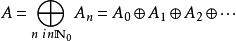 分次環論
分次環論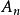 分次環論
分次環論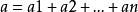 分次環論
分次環論成為一個分級的環。任何因素的元素 分解的被稱為 同質元件的 程度 Ñ。每個元件 一個的可以寫成的總和 與所有 一個a不同的均勻的元件 A。這 一個被稱為 均一組分的 a。
一些基本屬性是:
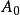 分次環論
分次環論是 A的一個子環;特別地,加法度量0和乘法式1是零度的齊次元素。
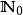 分次環論
分次環論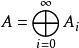 分次環論
分次環論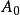 分次環論
分次環論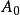 分次環論
分次環論交換環形 環 是一個諾埃利亞環當然如果 是Noetherian, A是有限生成的代數 。
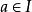 分次環論
分次環論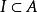 分次環論
分次環論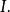 分次環論
分次環論 分次環論
分次環論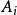 分次環論
分次環論 分次環論
分次環論一個理想的 如果每一個元素都是 同質的,其同質成分也屬於 (等價地,它們是 A的分級子模組;參見§分級模組)。 與 被稱為 均質部件的 。齊次理想是其均質部分的直接和 。
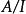 分次環論
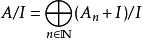
分次環論如果 我是 A的同質理想,那么 也是一個分級的環,並已分解
 分次環論
分次環論分級模組
模組理論中的相應思想是一個 分級模組,即分級環 A上的左模組 M也是這樣
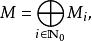 分次環論
分次環論和
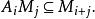 分次環論
分次環論例如:一個漸變向量空間是一個欄位上的漸變模組的示例(欄位具有平凡的分級)。
例如:分級環是一個分級模組。若且唯若它是分級子模組時,分級環中的理想是均勻的。分級模組的殲滅者是一個同質的理想。
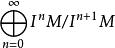 分次環論
分次環論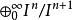 分次環論
分次環論例如:給定交換環 R和 R模組 M的理想 I, 是相關分級環上的分級模組 。
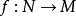 分次環論
分次環論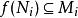 分次環論
分次環論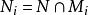 分次環論
分次環論一種態度 在分級模組之間,稱為 分級態射,是一種尊重分級的基本模組的態射;即 。甲 分級子模組是一個輔助模組是在自己的權利的分級模組,並且使得集合論夾雜物是分級模組的態射。顯式地,分級模組 N是 M的分級子模組,若且唯若它是 M的子模組並且滿足 。核心和漸變模組的態射圖像是分級的子模組。
備註:從漸變環到漸變環的漸變態,其圖像位於中心,這與將漸變代數的結構賦予後一個環相同。
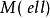 分次環論
分次環論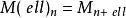 分次環論
分次環論由於分級模組 M,時, ℓ的捻合 是由...定義的分級模組 。(參見塞爾的代數幾何中的扭曲捆)
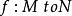 分次環論
分次環論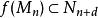 分次環論
分次環論設 M和 N為分級模組。如果 是模組的態射,然後 ˚F據說有度 d是否 。微分幾何中的微分形式的外部導數是這樣的具有次數1的態射的例子 。