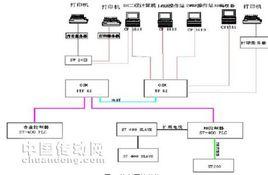
概念
分布參數控制系統(distributed parameter con-trol system)含控制作用的分布參數系統。泛指用分布參數系統描述的受控對象的控制,控制的目的是改變系統的性能品質,以適合人們的需要。例如,使不穩定的系統達到穩定,採用的方法可以是反饋鎮定,或最優控制(時間最省、能量最省等).控制作用可以是點控制、分布控制、邊界控制等。
在工程控制系統中,常常要求一個控制系統具有穩定性能。為了提高控制系統的性能,在現代控制技術中,經常採用閉環控制系統,也就是要設計一個反饋控制系統,使得一個開環控制系統同一個反饋控制器閉合後變為閉環控制系統具有近穩定性。
工作原理
分布參數環節的數學描述
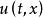 分布參數控制系統
分布參數控制系統具有分布參數特性的物質運動,其運動狀態不僅依賴於時間,而且還依賴於空間變數。例如橫向振動的弦,它的橫向位移,既是時間t又是弦上不同點位置x的函式。不同的時間,弦的位移是不同的,即使同一時間,在弦的不同點x處的位移也不同。在工程上,所有具有分布參數特性的對象和元件,都有著同樣的性質。描述這類對象的運動方程是偏微分方程或積分方程。
從工程技術上來說,所謂分布參數受控對象和元件,即分布參數環節,就是指其運動方程是由上述各類偏微分方程描述的。這些描述運動的方程式也叫發展方程。如果方程和邊界條件都是線性的,則這個環節叫作線性環節。
邊界條件反映了物體運動過程中,加在其邊界上的約束。不同的約束條件,其運動規律也不一樣。當初始條件和邊界條件都給定以後,方程的解才能唯一確定,這在數學中叫作偏微分方程的定解問題,而初始條件和邊界條件叫作定解條件。給定了運動方程,它描述了物體的一般運動,在方程和定解條件都給定的情況下,方程的解救描述了物體的一類特殊運動。
受控對象的分析
在受控對象的分析中,我們能夠遇到的有三種問題,即初值問題,邊值問題,混合問題。
所謂初值問題(柯西問題)是指只有初始條件就可定解。這類問題描述的是相當於空間變數的變化區域為無限大時的動態過程。它往往出現在雙曲線和拋物型方程中,如無限長圓柱體的扭轉振動,無限大介質中的熱傳導,無限長電力線的傳輸等。所謂無限大的區域,是指當物體的體積很大,而所要研究的問題是在較短時間裡,較小範圍內的變化規律。
邊值問題是在定解條件中只有邊界條件,沒有初始條件。這類問題描述的是運動的穩態過程。邊值問題往往出現在橢圓型方程中。
混合問題是在定解條件中既有初始條件也有邊界條件。這類問題描述了空間區域為有限時的動態過程。它大多出現在雙曲型和拋物型方程中。