分子軌道圖形理論
分子圖中的點(字母)表征原子,邊(鍵)代表原子間的成鍵作用。這種直觀圖像在現代量子化學形式體系中得到了某些保留。對於簡單的休克爾分子軌道法,主要的表述形式可建立在分子圖的基礎上,稱作分子軌道圖形理論。在休克爾分子軌道法中,本徵多項式占據重要地位,它是久期方程的冪展開式,多項式的根及對應本徵向量,就是共軛分子能級和軌道。本徵多項式是一種圖不變數,不因圖中點的標號不同而變,僅由分子圖本身確定。推算本徵多項式的圖的規則有多種,其中有效的一種是基於分子增大時的遞推關係式。設所討論的是直鏈多烯烴,碳原子數為n,分子圖對應直鏈碳骨架,即:
 分子軌道圖形理論
分子軌道圖形理論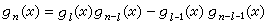 (1)
(1)
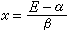 (2)
(2)
g1(x)=x g2(x)=x2-1
則有(已知g0=1):g3(x)=g1(x)g2(x)-g1(x)=x3-2x
式(1)的更深刻含義是:左端代表分子整體,右端的第一項代表一個鍵被斷裂,第二項代表斷裂鍵被抽去。更普遍的遞推關係由以下定理表述:一個共軛分子,圖形為G,斷裂一條邊,生成圖形G′,去掉經過斷裂邊的所有閉途徑(指從一點出發,經過不重複的點回到出發點的途徑),生成圖形G1、G2、… ,它們的本徵多項式P(x)滿足: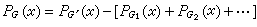 (3)
(3)
不僅本徵多項式,其他圖不變數也存在類似的圖形關係。目前討論得比較清楚,並已獲得嚴格的或近似嚴格結果的有:分子軌道係數、鄰接矩陣行列式aN 凱庫勒構式數、最高占據和最低空軌道能級、總能量等。利用這些結果,可對共軛分子有關性質作出解釋或預測,包括協同反應對稱守恆原理、芳香性、反應活性及同系線性規律等。

