說明
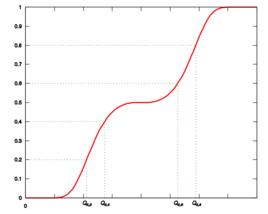
對Quartile的說明:
Quartile(四分位數):
第0個Quartile實際為通常所說的最小值(MINimum)
第1個Quartile(En:1st Quartile)
第2個Quartile實際為通常所說的中分位數(中數、二分位分、中位數:
Median)
第3個Quartile(En:3rd Quartile)
第4個Quartile實際為通常所說的最大值(MAXimum)
我想大家除了對1st、3rd Quartile不了解外,對其他幾個
統計量的求法都是比較熟悉的了,而求1st、3rd是比較
麻煩的,下面以求1rd為例:
設樣本數為n(即共有n個數),可以按下列步驟求1st Quartile:
(1)將n個數從小到大排列,求(n-1)/4,設商為i,餘數為j
(2)則可求得1st Quartile為:(第i+1個數)*(4-j)/4+(第i+2個數)*j/4
例(已經排過序啦!):
1.設序列為{5},只有一個樣本則:(1-1)/4 商0,餘數0
1st=第1個數*4/4+第2個數*0/4=5
2.設序列為{1,4},有兩個樣本則:(2-1)/4 商0,餘數1
1st=第1個數*3/4+第2個數*1/4=1.75
3.設序列為{1,5,7},有三個樣本則:(3-1)/4 商0,餘數2
1st=第1個數*2/4+第2個數*2/4=3
4.設序列為{1,3,6,10},四個樣本:(4-1)/4 商0,餘數3
1st=第1個數*1/4+第2個數*3/4=2.5
5.其他類推!
因為3rd與1rd的位置對稱,這是可以將序列從大到小排(即倒過來排),
再用1rd的公式即可求得:
例(各序列同上各列,只是逆排):
1.序列{5},3rd=5
2.{4,1},3rd=4*3/4+1*1/4=3.25
3.{7,5,1},3rd=7*2/4+5*2/4=6
4.{10,6,3,1},3rd=10*1/4+6*3/4=74=64.{10,6,3,1},3rd=10*1/4+6*3/4=7