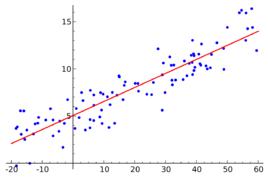
簡介
分位數回歸（英語： Quantile regression）是回歸分析的方法之一。最早由Roger Koenker和Gilbert Bassett於1978年提出。
一般地，傳統的回歸分析研究自變數與因變數的條件期望之間的關係，相應得到的回歸模型可由自變數的估計因變數的條件期望；分位數回歸研究自變數與因變數的條件分位數之間的關係，相應得到的回歸模型可由自變數估計因變數的條件分位數。相較於傳統回歸分析僅能得到因變數的中央趨勢，分量回歸可以進一步推論因變數的條件機率分布。分量回歸屬於非參數統計方法之一。
回歸分析
回歸分析（英語：Regression Analysis）是一種統計學上分析數據的方法，目的在於了解兩個或多個變數間是否相關、相關方向與強度，並建立數學模型以便觀察特定變數來預測研究者感興趣的變數。更具體的來說，回歸分析可以幫助人們了解在只有一個自變數變化時因變數的變化量。一般來說，通過回歸分析我們可以由給出的自變數估計因變數的條件期望。
分位數回歸模型
分位數回歸模型 分位數回歸模型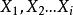
分位數回歸模型回歸分析是建立因變數（或稱依變數，反應變數）與自變數（或稱獨變數，解釋變數）之間關係的模型。簡單線性回歸使用一個自變數，復回歸使用超過一個自變數（）。
起源
回歸的最早形式是最小二乘法，由1805年的勒讓德(Legendre)，和1809年的高斯(Gauss)出版。勒讓德和高斯都將該方法套用於從天文觀測中確定關於太陽的物體的軌道（主要是彗星，但後來是新發現的小行星）的問題。 高斯在1821年發表了最小二乘理論的進一步發展，包括高斯－馬爾可夫定理的一個版本。
“回歸”（或作“回歸”）一詞最早由法蘭西斯·高爾頓（Francis Galton）所使用。他曾對親子間的身高做研究，發現父母的身高雖然會遺傳給子女，但子女的身高卻有逐漸“回歸到中等（即人的平均值）”的現象。
在1950年代和60年代，經濟學家使用機械電子桌面計算器來計算回歸。在1970年之前，它有時需要長達24小時從一個回歸接收結果。
回歸分析原理
•目的在於找出一條最能夠代表所有觀測資料的函式（回歸估計式）。
•用此函式代表因變數和自變數之間的關係。
回歸模型
回歸模型主要包括以下變數：
未知參數，記為 β，可以代表一個標量或一個向量。
•自變數，X。
•因變數，Y。
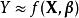分位數回歸模型回歸模型將Y和一個關於 X和 β的函式關聯起來：。
參閱
•曲線擬合
•估計理論
•廣義線性模型
•多元常態分配
•皮爾遜積矩相關係數
•信號處理
•相關分析
•多變數統計
