凸性不等式

凸性不等式（convexity inequality）是凸函式滿足的不等式，也常稱為延森不等式。

簡介

凸性不等式是凸函式滿足的不等式。

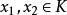凸性不等式

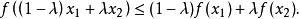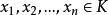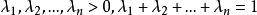凸性不等式

凸性不等式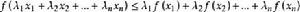

凸性不等式

凸性不等式

設f為實線性空間 X 的凸集 K 上的凸函式，即對於任何 和任何 λ>0，f滿足 逐次套用這一不等式，可以得到：對於任何 ，和任何 有

這個不等式即凸性不等式，也常稱為延森不等式。

推廣

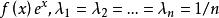凸性不等式

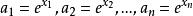凸性不等式

當 ，並且令 ，上式變為“幾何平均不大於算術平均”不等式：

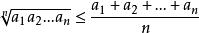凸性不等式

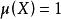凸性不等式

延森不等式的積分形式在套用上極為重要，設μ 是σ 代數 X 上的正測度， ，φ 關於μ 可積，f 是凸函式，則有延森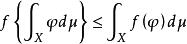不等式

凸性不等式

許多著名的不等式都是延森不等式的特例。

凸函式

凸函式是數學函式的一類特徵。凸函式就是一個定義在某個向量空間的凸子集C（區間）上的實值函式。

凸函式是一個定義在某個向量空間的凸子集C（區間）上的實值函式f，而且對於凸子集C中任意兩個向量, f((x+x)/2)>=(f(x)+f(x))/2，則f(x)是定義在凸子集c中的凸函式（該定義與凸規劃中凸函式的定義是一致的，下凸）。