一般定義
當兩個債券的久期相同時,它們的風險不一定相同,因為它們的凸性可能是不同的。在收益率增加相同單位時,凸性大的債券價格減少幅度較小;在收益率減少相同單位時,凸性大的債券價格增加幅度較大。因此,在久期相同的情況下,凸性大的債券其風險較小。數學上講, 凸性是債券價格對到期收益率二次微分,再除以債券價格,或者說是個二階導數。
是對債券價格曲線彎曲程度的一種度量。嚴格地講,凸性是指債券到期收益率發生變動而引起的債券價格變動幅度的變動程度。凸性是指債券價格對收益率的二階導數。凸性越大,債券價格曲線彎曲程度越大,用修正久期度量的利率風險所產生的誤差越大。凸性也是對債券久期對利率敏感性的測量。在價格—收益率出現大幅度變動時,它們的波動幅度呈非線性關係,由久期作出的預測將有所偏離。凸性就是對這個偏離的修正。
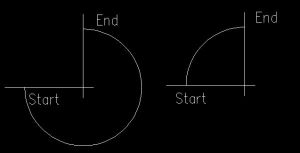
CADlisp定義
凸度定義
設圓弧所包含的圓心角為A(弧度表示),則凸度=四分之一圓心角之正切值
lisp表示
(setq 凸度 ((sin ( A / 4.0)) / (cos ( A / 4.0))))
C#表示
凸度=sin(A/4)/cos(A/4)
凸度值的範圍即sin(A/4)/cos(A/4)的取值範圍,A=0~2*PI
0到正無究,當A=360時,cos90=0,所以值無效
凸度的正負表明弧的方向