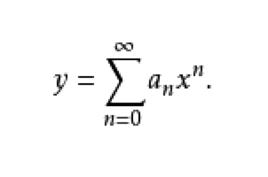一階微分方程的冪級數求解
基本方法
求
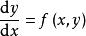 冪級數解法
冪級數解法 冪級數解法
冪級數解法滿足初始條件 的特解,其中
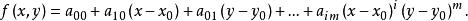 冪級數解法
冪級數解法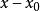 冪級數解法
冪級數解法我們假設所求的特解可展開成 的冪級數:
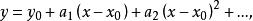 冪級數解法
冪級數解法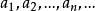 冪級數解法
冪級數解法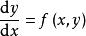 冪級數解法
冪級數解法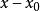 冪級數解法
冪級數解法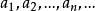 冪級數解法
冪級數解法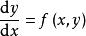 冪級數解法
冪級數解法 冪級數解法
冪級數解法其中, 是待定係數,把上式代入 中便得一恆等式,比較所得恆等式兩端的同次冪的係數,就可定出常數 ,以這些常數為係數的級數在其收斂區間內就是方程 滿足初始條件 的特解。
例題解析
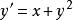 冪級數解法
冪級數解法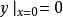 冪級數解法
冪級數解法例1 求方程 滿足 的特解。
 冪級數解法
冪級數解法解 由於 ,故設特解為
 冪級數解法
冪級數解法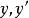 冪級數解法
冪級數解法把 的冪級數展開式代入原方程,得
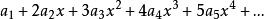 冪級數解法
冪級數解法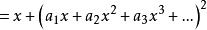 冪級數解法
冪級數解法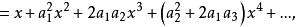 冪級數解法
冪級數解法比較x同次冪係數,得
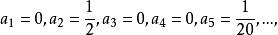 冪級數解法
冪級數解法故所求解的冪級數展開式的前幾項為
 冪級數解法
冪級數解法二階齊次線性方程的冪級數解法
定理
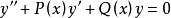 冪級數解法
冪級數解法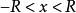 冪級數解法
冪級數解法若方程 中的係數P(x)與Q(x)可在 內展開為x的冪級數,則原方程必有如下冪級數解
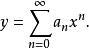 冪級數解法
冪級數解法求解方法
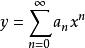 冪級數解法
冪級數解法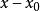 冪級數解法
冪級數解法設解為,將P(x),Q(x),f(x)展開為的冪級數,比較恆等式兩端x的同次冪係數,確定x。