定義
移位運算元
定義1 移位運算元（shift operator）：將希爾伯特空間中規範正交基的每一個基向量的位置向前(後)移動一位或若干位的線性運算元。
單側/雙側移位運算元
定義2 設H是復希爾伯特空間，{e}是H的規範正交基，由
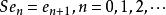移位運算元所確定的線性運算元S稱為 重複度為1的單側移位（或單側平移）運算元。
註：單側移位運算元是次正規運算元。
定義3 設H是復希爾伯特空間，{e}是H的一個規範正交基，由
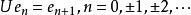移位運算元所確定的線性運算元稱為 重複度為1的雙側移位（或雙側平移）運算元。
定義4 設α是一個基數，α個重複度為1的單（雙）側移位運算元的正交和稱為 重複度為α的單（雙）側移位運算元。
註：單、雙側移位運算元統稱為移位運算元。
性質
1.S和U分別是重複度為α的單、雙側移位運算元時，S必是等距運算元，U必是酉運算元，且U必是S的正規擴張(當α有限時還是最小正規擴張).σ(S)={λ||λ|≤1}，σ(U)={λ||λ|=1}.
2.若S和U是重複度為1的移位運算元，則其共軛運算元由
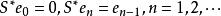移位運算元和
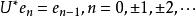移位運算元確定。
舉例
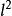移位運算元在 上定義運算元U：
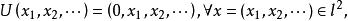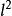移位運算元 移位運算元顯然，運算元U是 上的右移運算元。
推廣-加權移位運算元
加權移位運算元（weighted shift operator）是移位運算元的推廣，定義如下。
定義5 設H是希爾伯特空間，{e}是H的規範正交基，{w}...是一個數列，則由
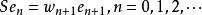移位運算元確定的線性運算元稱為 單側加權移位算子；而{wn}稱為S的 權序列。
設{e}是H的規範正交基，類似可定義權序列為{w}的 雙側加權移位運算元W：
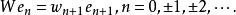移位運算元注 ：1.單、雙側加權移位運算元統稱加權移位運算元。
2.若S和W是重複度為1的加權移位運算元，則S和W的共軛運算元由
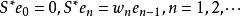移位運算元和
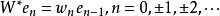移位運算元確定。
