共軛先驗
在貝葉斯統計中,如果後驗分布與先驗分布屬於同類,則先驗分布與後驗分布被稱為 共軛分布,而先驗分布被稱為似然函式的 共軛先驗。比如,高斯分布家族在高斯似然函式下與其自身共軛(自共軛)。這個概念,以及"共軛先驗"這個說法,由霍華德·拉法拉和羅伯特·施萊弗爾在他們關於貝葉斯決策理論的工作中提出。類似的概念也曾由喬治·阿爾弗雷德·巴納德獨立提出。
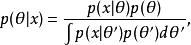 共軛先驗分布
共軛先驗分布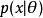 共軛先驗分布
共軛先驗分布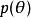 共軛先驗分布
共軛先驗分布具體地說,就是給定貝葉斯公式假定似然函式是已知的,問題就是選取什麼樣的先驗分布會讓後驗分布與先驗分布具有相同的數學形式。
共軛先驗的好處主要在於代數上的方便性,可以直接給出後驗分布的封閉形式,否則的話只能數值計算。共軛先驗也有助於獲得關於似然函式如何更新先驗分布的直觀印象。
所有指數家族的分布都有共軛先驗。
先驗機率
在貝葉斯統計中,某一不確定量p的 先驗機率分布是在考慮"觀測數據"前,能表達p不確定性的機率分布。它旨在描述這個不確定量的不確定程度,而不是這個不確定量的隨機性。這個不確定量可以是一個參數,或者是一個隱含變數(英語:latent variable)。
在使用貝葉斯定理時,我們通過將先驗機率與似然函式相乘,隨後標準化,來得到後驗機率分布,也就是給出某數據,該不確定量的條件分布。
先驗機率通常是主觀的猜測,為了使計算後驗機率方便,有時候會選擇共軛先驗。如果後驗機率和先驗機率是同一族的,則認為它們是共軛分布,這個先驗機率就是對應於似然函式的共軛先驗。
後驗機率
在貝葉斯統計中,一個隨機事件或者一個不確定事件的後驗機率是在考慮和給出相關證據或數據後所得到的條件機率。
假設一個學校里有60%男生和40%女生。女生穿褲子的人數和穿裙子的人數相等,所有男生穿褲子。一個人在遠處隨機看到了一個穿褲子的學生。那么這個學生是女生的機率是多少?
使用貝葉斯定理,事件A是看到女生,事件B是看到一個穿褲子的學生。我們所要計算的是P(A|B)。
P(A)是忽略其它因素,看到女生的機率,在這裡是40%
P(A')是忽略其它因素,看到不是女生(即看到男生)的機率,在這裡是60%
P(B|A)是女生穿褲子的機率,在這裡是50%
P(B|A')是男生穿褲子的機率,在這裡是100%
P(B)是忽略其它因素,學生穿褲子的機率,P(B) = P(B|A)P(A) + P(B|A')P(A'),在這裡是0.5×0.4 + 1×0.6 = 0.8.
根據貝葉斯定理,我們計算出後驗機率P(A|B):
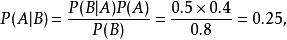 共軛先驗分布
共軛先驗分布可見,後驗機率實際上就是條件機率。
高斯分布
常態分配(德語: Normalverteilung;英語: normal distribution)又名 高斯分布(德語: Gauß-Verteilung;英語: Gaussian distribution, 以德國數學家卡爾·弗里德里希·高斯的姓冠名),是一個在數學、物理及工程等領域都非常重要的機率分布,由於這個分布函式具有很多非常漂亮的性質,使得其在諸多涉及統計科學離散科學等領域的許多方面都有著重大的影響力。比如圖像處理中最常用的濾波器類型為Gaussian濾波器(也就是所謂的常態分配函式)。
 共軛先驗分布
共軛先驗分布 共軛先驗分布
共軛先驗分布 共軛先驗分布
共軛先驗分布若隨機變數服從一個位置參數為、尺度參數為的機率分布,記為:
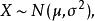 共軛先驗分布
共軛先驗分布則其機率密度函式為
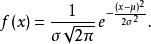 共軛先驗分布
共軛先驗分布 共軛先驗分布
共軛先驗分布 共軛先驗分布
共軛先驗分布 共軛先驗分布
共軛先驗分布常態分配的數學期望值或期望值等於位置參數,決定了分布的位置;其方差的開平方或標準差等於尺度參數,決定了分布的幅度。
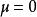 共軛先驗分布
共軛先驗分布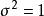 共軛先驗分布
共軛先驗分布常態分配的機率密度函式曲線呈鐘形,因此人們又經常稱之為 鐘形曲線(類似於寺廟裡的大鐘,因此得名)。我們通常所說的 標準常態分配是位置參數,尺度參數的常態分配。
參見
•中心極限定理
•機率論
•伽瑪分布
