貝塔(β,beta)分布
機率論中還有一種稱為貝塔(β,beta)分布的機率密度分布函式。它的數學形式是
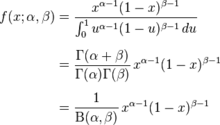 貝塔分布
貝塔分布,0<1, p>0,q>0 (18.25)
這裡的變數x僅能出現於0到1之間,p,q是兩個大於0的參數。B(p,q) 的含義是
(18.26)
它與Γ函式,有如下關係
(18.27)
而我們介紹過的階乘符號!與Γ的關係是
n!= Γ(n+1)
所以貝塔分布也可以寫為
(18.28)
現在考慮從最複雜原理加適當的約束條件推求這個機率密度分布函式的問題。根據過去的經驗,容易看出它可能是下面兩個約束條件與最複雜原理的套用結果。
變數x的對數的平均值為固定值(等價於幾何平均值為常數):
(18.29)
(1-x)的對數的平均值也是固定之值:
(18.30)
作為機率密度,當然還有
(18.31)
根據上面的三個約束公式和最複雜原理,利用拉哥朗日方法,構造的F函式是
求F對未知的機率密度f的偏微商,並且令它等於0(利用了最複雜原理),我們得到
利用分布函式的積分應當等於1的約束和積分知識我們得到
所以分布函式可以寫為
(18.32)
顯然,這個公式的外型已經與貝塔分布一致了。餘下的問題是利用關於u,v的約束公式可以求出C2,C3 。使這個公式通過u,v來表示。由於u,v與C2,C3的關係比較複雜,我們沒有得到具體的關係式。但是機率密度分布函式的形狀與機率論中的貝塔分布一致就已經達到了我們的目的:界於0-1之間的變數的兩種幾何平均值固定和最複雜原理相結合可能是一些貝塔分布形成的原因。
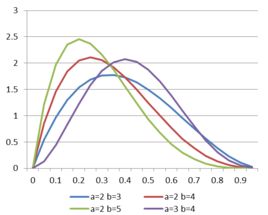
貝塔分布中的變數x的變化範圍僅能在0到1之間,而且(1-x)與x有對稱性,這是重要的特點。圖18.5給出了p=3,q=6時的貝塔分布函式的形狀。
圖18.5貝塔分布的曲線形狀
實例
空氣中含有的氣體狀態的水分。表示這種水分的一種辦法就是相對濕度。即現在的含水量與空氣的最大含水量(飽和含水量)的比值。我們聽到的天氣預告用語中就經常使用相對濕度這個名詞。
相對濕度的值顯然僅能出現於0到1之間(經常用百分比表示)。而空氣為什麼出現某個相對濕度顯然具有隨機性(可以利用最複雜原理),這些提示我們空氣的相對濕度可能符合貝塔分布。
馬淑紅等人完成的“塔里木氣候極值及其在油田工程設計中的套用”研究中(同名的書由氣象出版社於1995年出版見138-142頁),劉紹民等人分析了冬季塔里木盆地的日最大相對濕度和夏季日最小相對濕度。證實它們都符合貝塔分布。