定義
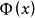 公倍式
公倍式 公倍式
公倍式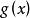 公倍式
公倍式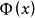 公倍式
公倍式 公倍式
公倍式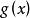 公倍式
公倍式若多項式 既是 的倍式,又是 的倍式,則 就稱為 與 的一個公倍式。
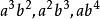 公倍式
公倍式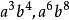 公倍式
公倍式例如: 的公倍式有 等 。
最低公倍式
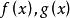 公倍式
公倍式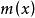 公倍式
公倍式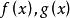 公倍式
公倍式設 是數域P上的兩個多項式,P上的多項式 稱為多項式 的 最 低公倍式,如果它滿足下面兩個條件:
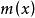 公倍式
公倍式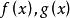 公倍式
公倍式(1) 是 的公倍式;
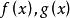 公倍式
公倍式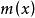 公倍式
公倍式(2) 的任一個公倍式都是 的倍式。
換句話說,即次數最低的公倍式。最低公倍式也稱最低公倍式。
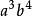 公倍式
公倍式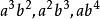 公倍式
公倍式例如上例中的 就是 的最低公倍式。
相關概念
因式與倍式
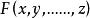 公倍式
公倍式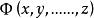 公倍式
公倍式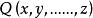 公倍式
公倍式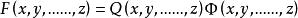 公倍式
公倍式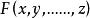 公倍式
公倍式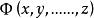 公倍式
公倍式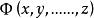 公倍式
公倍式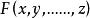 公倍式
公倍式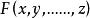 公倍式
公倍式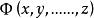 公倍式
公倍式給定數域F上的多項式 和 ,如果存在一個多項式 ,使恆等式 成立,就說多項式 能被多項式 整除,多項式 叫做多項式 因式(或因子)。多項式 叫做 的 倍式。
每一個異於零的數,以及每一個與給定的多項式只差一個非零的數值因子的多項式是給定多項式的因式。這些因式叫做給定多項式的 當然因式,給定多項式的一切其它的因式叫做 非當然因式。
公倍數
公倍數(common multipule)是兩個或兩個以上的數的共同的倍數。例如3、4、9的公倍數是36、72、…等。
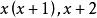 公倍式
公倍式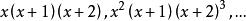 公倍式
公倍式如果兩個以上的整式都能整除某一整式,則後一整式稱為所給這些整式的 公倍式。例如, 的公倍式是 等。
公倍數(式)是最低公倍數(式)的倍數(式)。
公因式
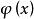 公倍式
公倍式 公倍式
公倍式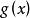 公倍式
公倍式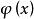 公倍式
公倍式 公倍式
公倍式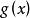 公倍式
公倍式若數域F上的多項式 既是 的因式,又是 的因式,則 就稱為 與 的一個公因式。
 公倍式
公倍式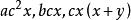 公倍式
公倍式例如: 是 的公因式。
最高公因式
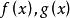 公倍式
公倍式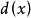 公倍式
公倍式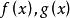 公倍式
公倍式設 是數域P上的兩個多項式,P上的多項式 稱為 的最高公因式,如果它滿足下面兩個條件:
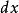 公倍式
公倍式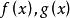 公倍式
公倍式(1) 是 的因式;
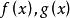 公倍式
公倍式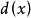 公倍式
公倍式(2) 的公因式全是 的因式。
換句話說,即次數最高的公因式。最高公因式也稱最大公因式。
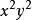 公倍式
公倍式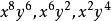 公倍式
公倍式例如: 是 的最高公因式 。

