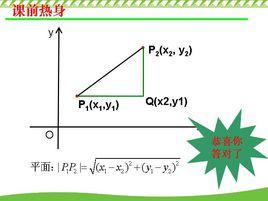
定義
兩點間距離公式常用於函式圖形內求兩點之間距離、求點的坐標的基本公式,是距離公式之一。兩點間距離公式敘述了點和點之間距離的關係。
平面坐標形式
下面不加證明地給出幾個公式。
公式
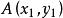 兩點間距離公式
兩點間距離公式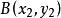 兩點間距離公式
兩點間距離公式設兩個點A、B以及坐標分別為 、 ,則A和B兩點之間的距離為:
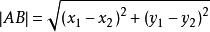 兩點間距離公式
兩點間距離公式推論
直線上兩點間的距離公式:
 兩點間距離公式
兩點間距離公式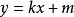 兩點間距離公式
兩點間距離公式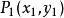 兩點間距離公式
兩點間距離公式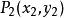 兩點間距離公式
兩點間距離公式設直線 的方程為 ,點 , 為該線上任意兩點,則
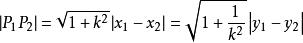 兩點間距離公式
兩點間距離公式 兩點間距離公式
兩點間距離公式這一公式即所謂圓錐曲線的弦長公式。若記 為直線AB的傾斜角,則
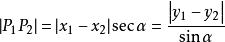 兩點間距離公式
兩點間距離公式同時,若已知直線公式和其中一個點,並且給定了距離,可以反求另一個點的坐標。
實例
現在有一隻工程隊要鋪設一條網路,連線A,B兩城。他們首先要知道兩城之間的距離,才能準備材料。他們用全球定位系統將兩城的位置在平面直角坐標系中表示出來。現在我們就來試試看能不能幫他們求出A、B兩城之間的距離。
在黑板上畫出A,B兩點,如下圖:
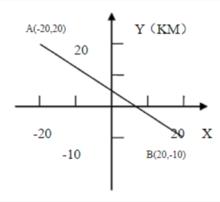 兩點間距離公式
兩點間距離公式那么,我們怎么求出AB之間的距離呢?
我們來試試看,能不能通過添加一些輔助線,來解答問題呢?
首先我們作點A關於X軸的垂線,設垂足為A’,再作B關於Y軸的垂線,設垂足為B’;延長AA’和BB’使之交與C點。
如下圖:
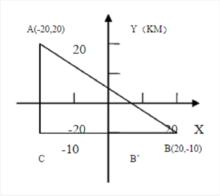 兩點間距離公式
兩點間距離公式顯然角C等於90度,這樣我們就構造出了一個三角形ABC,而我們要求的AB就在這
個直角三角形上。因此我們是不是可以考慮看看用勾股定理來求出AB呢?
由勾股定理可以得知:
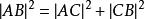 兩點間距離公式
兩點間距離公式由A(-20,20)和B(20,-10),所以可知C(-20,-10)。現在我們可以將AB平移到Y軸上,設這兩個對應的點為N1,N2,所以:
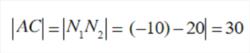 兩點間距離公式
兩點間距離公式因此可知:
AB =|20-(-20)| +|(-10)-20| =2500
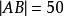 兩點間距離公式
兩點間距離公式所以。
現在,我們已經求出了A、B兩城的距離。現在,我們來思考一個問題:是不是任意兩點,只要知道這兩點的坐標,就可以求出這兩點之間的距離呢?我們能不能找到一個公式來求兩點之間的距離呢?
不妨設A(x1,x2),B(x2,y2)。因此可以推出
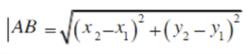 兩點間距離公式
兩點間距離公式三維坐標形式
公式
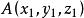 兩點間距離公式
兩點間距離公式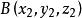 兩點間距離公式
兩點間距離公式設 , ,則
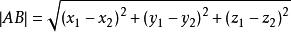 兩點間距離公式
兩點間距離公式推導過程
 兩點間距離公式
兩點間距離公式 兩點間距離公式
兩點間距離公式 兩點間距離公式
兩點間距離公式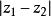 兩點間距離公式
兩點間距離公式在三維坐標中,首先計算兩點在平面坐標中(即 , 軸上)的距離,再計算兩點在 軸上的垂直距離 。再次用勾股定理,即證。
極坐標形式
公式
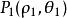 兩點間距離公式
兩點間距離公式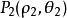 兩點間距離公式
兩點間距離公式下面不加證明地給出該公式。設極坐標系中兩點 , ,則
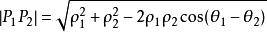 兩點間距離公式
兩點間距離公式