基本介紹
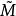全測地子流形 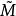全測地子流形 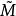全測地子流形
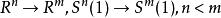全測地子流形全測地子流(totally geodesic submanifold)是一類子流形，指第二基本形式恆為零的子流形。設M為黎曼流形的黎曼子流形，則M為的全測地子流形的另一等價條件是：中的任意一條與M相切的測地線位於M中，且也為M的測地線。通常的包含嵌入都是全測地子流形的例子。全測地子流形的例子是十分稀少的，一般黎曼流形幾乎都不具有任何全測地子流形，黎曼流形的一個等距變換的固定點集是一個全測地子流形，具正里奇曲率流形的任意兩個緊緻全測地超曲面必相交 。
相關結論
關於全測地子流形有下面結果。
1. S是M的全測地子流形，則S 的測地線也是M的測地線。
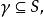全測地子流形
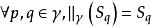全測地子流形2. Riemann流形M的連通完備子流形S是全測地子流形若且唯若沿S中曲線的M的平行移動總將S的切向量移動到S的切向量，即若則
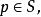全測地子流形
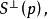全測地子流形3. M為單連通完備Riemann流形，且曲率為負。S 為M 的閉全測地子流形，則與S垂直於p的M的測地線構成M的一個子流形且
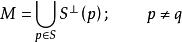全測地子流形
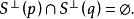全測地子流形時，
4. S為Riemann流形M的全測地子流形，如果M是局部對稱的，則S 也是局部對稱的。
事實上，S上的每個點的( 中心)測地對稱是M在該點的(中心)測地對稱在S 上的限制。
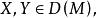全測地子流形
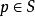全測地子流形
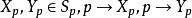全測地子流形
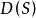全測地子流形
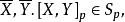全測地子流形
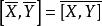全測地子流形5. 設S是M的子流形，使得時有為中元素，記為於是有。
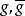全測地子流形
全測地子流形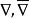
全測地子流形 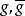全測地子流形
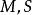全測地子流形
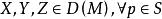全測地子流形
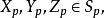全測地子流形又若M有Riemann結構為在S上誘導的Riemann結構，為對應的的Riemann聯絡，又均有則有
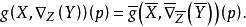全測地子流形
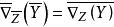全測地子流形又設S為M的全測地子流形，則有。
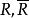全測地子流形 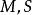全測地子流形又若分別為的曲率張量，則
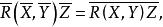全測地子流形
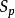全測地子流形而且，對上的一個二維子空間，關於M與S的截曲率是一樣的 。
對稱空間的全測地子流形
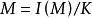全測地子流形
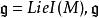全測地子流形
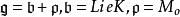全測地子流形
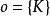全測地子流形 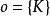全測地子流形
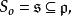全測地子流形定理 設是Riemann對稱空間，又對應Cartan分解為為的切空間，S是M的子流形，S在處切空間為於是有
1) 若S為M的全測地子流形，則有
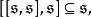全測地子流形
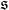全測地子流形 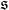全測地子流形
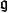全測地子流形滿足上述關係，稱為的一個 李三系。
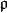全測地子流形 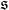全測地子流形
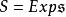全測地子流形2) 若中子空間滿足(1)，則是M的 全測地子流形 。
